Minterms, Maps, and Simplification
Tom Kelliher, CS 240
Feb. 3, 2010
How to order the rows of a truth table: 0 at the top; 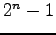 at
the bottom. Example: two-input AND.
at
the bottom. Example: two-input AND.
Read 2.5.
Written assignment: Some of the Boolean manipulation problems are tricky
-- start early.
Logic gates and Boolean algebra.
- Minterms and products
- Simplification using Karnaugh maps.
Karnaugh map manipulation; don't cares.
- What is a product? A sum?
- Definition of a minterm: A product term containing all literals,
complemented or not complemented.
Examples in three variables (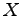 ,
, 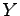 ,
, 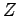 ). Identify which are minterms
and which are not:
). Identify which are minterms
and which are not: 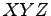 ,
,
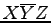 ,
, 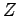 ,
, 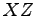 .
.
- Sum of minterms. Can be derived directly from a truth table.
Example: sum output of a full binary adder. Derive truth table and sum
of minterms equation. Observe
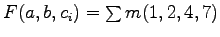 and
relationship to even parity (exclusive or).
and
relationship to even parity (exclusive or).
- Product of sums form and difference from sum of minterms (products).
- A graphical tool for minimizing sum of minterm expressions.
- Two-variable maps:
- Structure; literal and value labels.
- Theory: Show simplification of
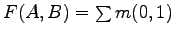 given
Actual Karnaugh map:
given
Actual Karnaugh map:
| |
 |
| |
0 |
1 |
 |
0 |
1 |
1 |
| |
1 |
0 |
0 |
- Three-Variable maps:
- Structure and connectivity.
- Examples: Sum and carry-out of full binary adder.
- Four-Variable maps:
- Structure and connectivity.
- Example: Product bit 1 of two-bit multiplier. (Start with
``product'' table and then produce truth table for bit 1.)
- Five-Variable maps? Higher?
Thomas P. Kelliher
2010-02-02
Tom Kelliher
![]() at
the bottom. Example: two-input AND.
at
the bottom. Example: two-input AND.
![]() ,
, ![]() ,
, ![]() ). Identify which are minterms
and which are not:
). Identify which are minterms
and which are not: ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
![]() and
relationship to even parity (exclusive or).
and
relationship to even parity (exclusive or).