Vector and Affine Spaces, Frames, and Homogeneous Coordinates
Tom Kelliher, CS 320
Apr. 10, 2009
Read Chapter 5.
Animating the color cube.
- Introduction.
- Vector spaces, affine spaces, lines.
- Affine sums and convex hulls.
- The plane and normal vectors.
- Coordinate systems and frames.
- Homogeneous Coordinates
Viewing
Properties of scalars, points, vectors.
Uses in graphics?
- Two entities: scalars, vectors.
- Defined operations: scalar-vector multiplication, vector-vector
addition.
Examples.
- Vector space plus.
- Additional object: point.
- Additional operation: vector-point addition, yielding a point.
Equivalently, point-point subtraction, yielding a vector.
Examples.
Consider:
where 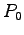 is an arbitrary point,
is an arbitrary point, 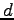 is an arbitrary vector, and
is an arbitrary vector, and 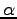 is a scalar.
is a scalar.
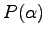 is what?
is what?
What happens when we vary 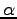 ? -- Parametric form of the line.
? -- Parametric form of the line.
- No point-point addition or scalar-point multiplication. But...
- For a point
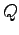 , vector
, vector 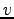 , and scalar
, and scalar 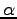
But we can find 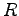 such that:
such that:
So:
- If we extend this to
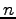 points:
points:
where
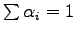 and
and
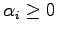 then we get the convex
hull of the points.
then we get the convex
hull of the points.
- The plane can be parametrically defined by a point and two
non-parallel vectors:
or
- Find a normal vector:
So:
- This is another parametric form of the plane.
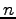 is normal to that
plane.
is normal to that
plane.
- Vectors have no positions, although we often think they do.
- For transformation purposes, we want to represent a graphical point
as a vector relative to an origin.
- A frame is a vector basis and a reference point (origin):
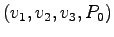 .
.
- Any point can be represented:
- Any vector can be represented:
- Ambiguous as to whether an object is a point or a vector.
- Transformations are accomplished by changing the basis. From
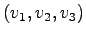 to
to
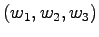 .
.
How is this done for scaling and rotation? Translation? (Everything is
relative to original origin in matrix multiplications.)
How does this affect a point in the original frame?
- Explicitly include the origin in the point/vector representation:
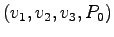 .
.
Change basis to
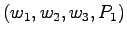
- Point, vector representations are different
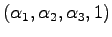 ,
,
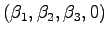 .
.
Thomas P. Kelliher
2009-04-10
Tom Kelliher
![]() is what?
is what?
![]() ? -- Parametric form of the line.
? -- Parametric form of the line.
![]()