| Modus Ponens |
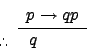
|
| Modus Tollens |
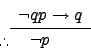
|
| Hypothetical Syllogism |
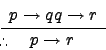
|
| Disjunctive Syllogism |
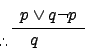
|
| Addition |
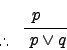
|
| Simplification |
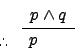
|
| Conjunction |
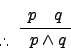
|
| Resolution |
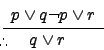
|
Tom Kelliher, MA 190
Feb. 8, 2008
| Modus Ponens |
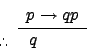
|
| Modus Tollens |
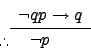
|
| Hypothetical Syllogism |
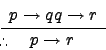
|
| Disjunctive Syllogism |
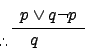
|
| Addition |
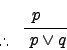
|
| Simplification |
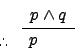
|
| Conjunction |
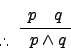
|
| Resolution |
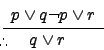
|
| Universal instantiation |
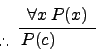
|
| Universal generalization |
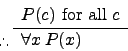
|
| Existential instantiation |
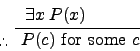
|
| Existential generalization |
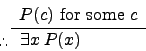
|
| Universal modus ponens |
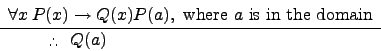
|
| Universal modus tollens |
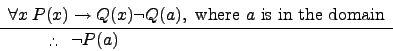
|
pp. 72-74: 1; 3 d, e; 5; 7; 14 c; 23; 27.