Routing Algorithms

Tom Kelliher, CS 325

Apr. 25, 2008

Administrivia

Announcements

Assignment

Read 4.6.

From Last Time

IP protocol.

Outline

1. Introduction.

2. Link state routing.

3. Distance vector routing.

4. Hierarchical routing.

Coming Up

Routing in the Internet.

Introduction

1. Host-to-host routing boils down to source router-to-destination router routing.

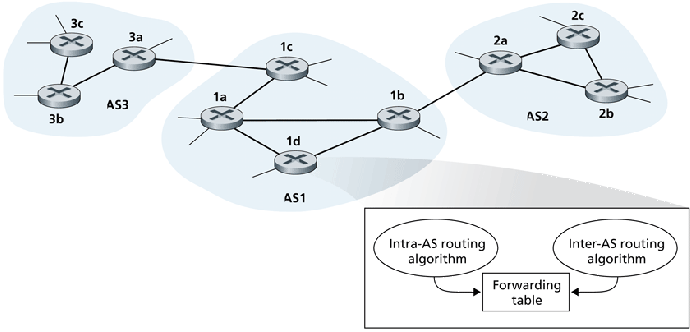
   Hence, we only need consider routing between routers.

2. Routing algorithms represent networks as graphs.

3. Let's recall a few things about graphs:
   1. A set of vertices/nodes representing the routers.

   2. A set of labeled edges, representing the links between routers. The edge labels specify the cost of the link.

   3. Several ways to assign link costs:
      1. Assign a cost of 1 to every link.

         Minimizes hop count.

      2. Assign cost as the inverse of link speed.

         Maximizing use of high speed links.

      3. Assign costs for political/business reasons.

         Discourage use of certain links.

   4. A path/route is an ordered list of connected vertices, from source to destination:
      1. Path cost is the sum of the edge costs along the path.

      2. Routing algorithms work to minimize all path costs.

   Example network represented as a graph:

   

4. Classifications of routing algorithms:
   1. Global: the routing algorithm knows the connectivity status and cost of all links in the network.

      The algorithm might be run at one centralized location or multiple sites.

      Referred to as link state algorithms.

      How is link state information acquired? How much overhead in acquiring this information?

   2. Decentralized: the routing algorithm runs in an iterative, distributed manner within each router.

      Routers only know the cost of their directly-connected links, and share routing information with their neighbors.

      After a number of iterations, routers converge on the least-cost routes.

      Referred to as distance vector algorithms, as routers maintain a vector of distances (costs) to other routers.

Link State Routing

1. A router periodically broadcasts link state information to all other routers in the network.

2. Routers periodically run the LS algorithm to update their forwarding tables.

3. Dijkstra's algorithm is generally used. The following notation is used below:
   1. N -- the set of the graph's vertices.

   2. N' -- set of vertices for which we know the final least-cost paths.

   3. c(u, v) -- the cost associated with the edge from u to v.

      If no such edge exists, the cost is infinity.

      c(u, v) could differ from c(v, u).

   4. D(v) -- current cost of the least-cost path from the source vertex to vertex v.

   5. f(v) -- first vertex, connected to the source vertex, along the current least cost path from the source vertex to v.

      f(v) will be the first-hop router for forwarding.

      This differs slightly from the algorithm given in the textbook, which stores the next-to-last vertex along the path in p(v), requiring post-processing to determine the first-hop routers.

   The algorithm:

   N' = {u};   // u is the source vertex.
   for each vertex, v, in N
      D(v) = c(u, v);
      if c(u, v) is finite   // D(v) is finite only for u's neighbors.
         f(v) = v;
   
   do
      find w not in N' such that D(w) is a minimum;
      add w to N';
      for each neighbor, v, of w that is not in N'
         if D(w) + c(w, v) < D(v)
            D(v) = D(w) + c(w, v);
            f(v) = f(w);
   while (N' != N);
   

   An efficient implementation will be ${\rm O}(n \log n)$. (A poor implementation would be ${\rm O}(n^2)$, emphasizing the importance of paying attention in algorithms class!)

4. Run the algorithm on this graph:
   

   This will be the result:

   

Anomalous LS Routing

Oscillations can occur if link cost is based on link traffic. Consider this example:

1. x and z route one unit of traffic to w; y routes $e$ units of traffic to w. x and z route directly to w; y routes via x.

   (Assume that this traffic density is repeated for each routing cycle.)

   

2. After running the LS algorithm, the least cost path is now clockwise.
   

3. After running the LS algorithm again, the least cost path is now counter-clockwise!
   

4. Clockwise, again!!
   

5. Basing routing decisions on link traffic is desirable. Routing oscillations are not desirable.

   A solution to this problem is to prevent the routers from running the routing algorithm simultaneously. If this is not done carefully, the routers will tend to self-synchronize.

Distance Vector Routing

1. The DV algorithm is distributed, asynchronous, and self-terminating.

   It iterates until it converges upon the shortest paths, at which time it ceases execution, until a link cost changes.

2. Notation:
   1. d_x(y) is the cost of the least-cost path from x to y.

   2. The Bellman-Ford equation recognizes that

         d_x(y) = min_v{c(x, v) + d_v(y)}
      

      where min_v{} is taken over all of x's neighbors.

      This equation is the heart of the DV algorithm.

3. DV_x = {D_x(y): y in N} is the vector of estimated least-cost distances from x to all vertices y in N.

   Over time, these estimates converge upon the actual least-cost distances.

4. DV algorithm for vertex x:

   for all vertices y in N
      D_x(y) = c(x, y);   // If x and y aren't neighbors, this cost is
                          // infinity. 
   
   for each neighbor w and all vertices y
      D_w(y) = infinity;
   
   for each neighbor w
      send DV_x to w;
   
   while true
      wait until a link cost to a neighbor w changes or a neighbor w
         sends a new distance vector;
   
      for each y in N
         D_x(y) = min_v{c(x, y) + D_v(y)};
   
      if D_x(y) changed for any vertex y
         for each neighbor w
            send DV_x to w;
   

5. Example:
   

Anomalous Behavior in DV Routing

Consider the following link cost changes, ignoring x:

1. Left figure -- link cost decrease: y updates, sends; z updates, sends; done.

   Two iterations.

2. Right figure -- link cost increase: This will take $50 -4 = 46$ message exchanges before the forwarding tables stabilize. Meanwhile, we have a routing loop between y and z for datagrams destined for x.

   -- ``Count to infinity'' problem.

   This specific problem can be fixed if z reports to y that its distance to x is infinity. In general, if a uses b to route to c, a should report to b that its distance to c is infinity -- eliminating such routing loops.

   -- ``Poisoned reverse.''

   Unfortunately, poisoned reverse doesn't work for routing loops involving three or more routers.

Comparing LS and DV Algorithms

1. LS requires more message exchanges than DV.

2. LS converges more quickly than DV. DV can suffer from routing loops until it does converge and suffers from count-to-infinity.

3. Both algorithms have failure modes, but LS failures tend to be local, while DV failures can be network-wide.

Hierarchical Routing

1. Routing is done in a hierarchical manner:
   1. To control scale. Number of Internet routers would overflow forwarding tables.

      LS info exchanges would be prohibitive. DV algorithms would never converge.

   2. To allow administrative autonomy. An ISP should be able to control its routers -- using whatever routing protocol it chooses.

      ISPs should be able to hide details of their networks from each other.

2. Organize routers into autonomous systems.
   1. Routers within an AS run the same routing protocol.

   2. Routers that route between ASs are called gateway routers.

3. Example:
   

   Within an AS, LS or DV algorithms are used.

   Between AS's, network connectivity information is exchanged. This info must be propagated from the gateway routers to the interior routers.

4. If a foreign network is reachable through multiple gateways, interior routers use ``hot potato'' routing to route to the nearest gateway:
   

5. An ISP may treat its system as a single AS, or it may partition it into multiple ASs.

Tom Kelliher