Addition Limits
Tom Kelliher, CS 240
Feb. 20, 2008
Decoders, encoders, muxes.
- A ``fast binary adder.''
- The lower bound for addition speed.
Carry lookahead addition, other integer representations.
- Ripple carry adder: example of reuse and divide and conquer.
- Wire together
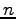 full binary adders in order to add two
full binary adders in order to add two 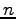 bit
numbers.
bit
numbers.
- Running time of a ripple carry adder.
Running time of a full binary adder is O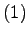 . Ripple carry adder?
. Ripple carry adder?
Excessive!!!
- An O
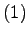 (!!!)
(!!!) 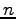 bit adder.
bit adder.
- Important equations (briefly explain):
Carry generate at bit position 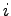 :
: 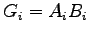 .
.
Carry propagate at position 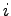 :
:
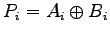 .
.
- Carry-in is
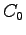 .
.
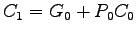 .
.
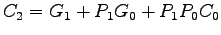 .
.
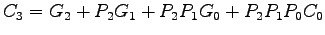 .
.
Etc.
- What's the circuit depth of
 ?
?
- What's wrong with this picture?
- Due to Winograd.
- Our abstract gate for an idealized adder: the
 gate
gate
- Independent of technology.
 is the fan-in.
is the fan-in.
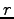 is the radix (binary).
is the radix (binary).
- Assume that such a gate can compute any
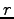 -valued function of
-valued function of 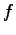 inputs.
inputs.
- Adding
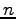 bit numbers. How many inputs? How many outputs? What is
the minimum number of inputs some output is dependent upon? The
maximum?
bit numbers. How many inputs? How many outputs? What is
the minimum number of inputs some output is dependent upon? The
maximum?
- For the output dependent upon that maximum, consider the ideal
circuit which reduces its inputs to the final output.
- What does it look like?
- How many intermediate signals remain after one level of gates?
- What is its depth? -- That's the lower bound for addition.
Thomas P. Kelliher
2008-02-18
Tom Kelliher
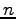 full binary adders in order to add two
full binary adders in order to add two 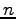 bit
numbers.
bit
numbers.
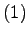 . Ripple carry adder?
. Ripple carry adder?
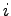 :
: 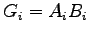 .
.
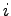 :
:
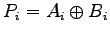 .
.
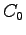 .
.
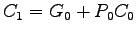 .
.
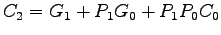 .
.
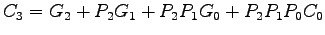 .
.
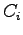 ?
?