Unifying SQL, Relational Algebra, and the Calculi
Tom Kelliher, CS 318
Mar. 4, 2002
Formal specification due Friday. What I expect.
Read 8.1--4. Bring hard hats and safety glasses.
DRC.
- Understanding SQL through TRC.
- Relationship between relational algebra and calculi.
Normalization theory, functional dependencies.
- How do we verify that an SQL query will do what we want it to do?
The translation to English isn't all that clear.
- What does it mean for an SQL query to agree with its English
description? Both must hold:
- Every tuple produced by the SQL must satisfy the English
description.
- For every tuple, t, which satisfies the English description,
there is a way to assign tuple variable to the SQL query so that the
query target is t.
(Subsets of each other.)
- Idea: mechanically translate SQL to TRC. TRC is ``easy'' to
understand.
Examples. What's the English translation of each of the following?
- Simple, single table.
SELECT T.Id
FROM Transcript T
WHERE T.CrsCode = 'CS318' AND T.Semester = 'S2002';
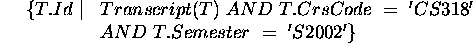
- Simple, two tables, single query target.
SELECT S.Name
FROM Student S, Transcript T
WHERE S.Id = T.Id AND T.CrsCode = 'CS318' AND T.Semester = 'S2002';
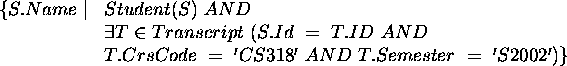
How would this change if we added Grade to the query target?
- More complex, uncorrelated sub-query.
SELECT T.Id
FROM Transcript T
WHERE T.CrsCode IN (SELECT C.CrsCode
FROM Course C
WHERE C.DeptId = 'CS');
Translate using a view for the sub-query:
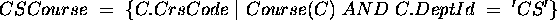
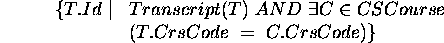
Modify to retrieve names.
- More complex, correlated sub-query.
SELECT R.StuId, P.Id, R.CrsCode
FROM Transcript R, Professor P
WHERE R.Semester <> 'S2002'
AND R.CrsCode IN (SELECT T.CrsCode
FROM Teaching T
WHERE T.ProfId = P.Id
AND T.Semester = 'S2002');
Again, use a view:
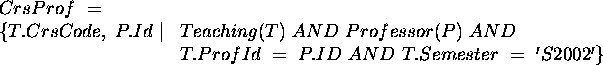
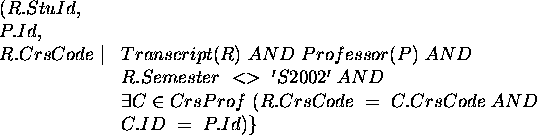
- Equivalent under domain independence.
In plain English, they're equivalent when queries depend upon only the
tuples found in a set of relations, not tuples outside the set.
- Ullman showed how to reduce calculi queries to relational algebra.
- Reducing relation algebra queries to TRC:
- Selection: reduce
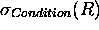 .
.
- Projection: reduce
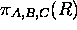 .
.
- Cartesian Product: reduce
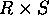 . (Assume R has
attributes A, B, C and S has attributes D and E.
. (Assume R has
attributes A, B, C and S has attributes D and E.
- Union: reduce
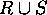 .
.
- Set difference: reduce R - S.
- Division: ``No discussion of relational algebra is complete
without saying something about the division operator.''
Thomas P. Kelliher
Sun Mar 3 15:58:22 EST 2002
Tom Kelliher
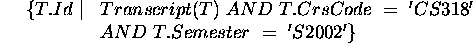
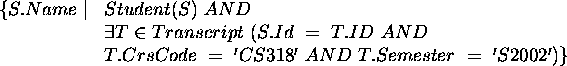
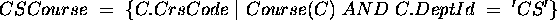
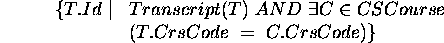
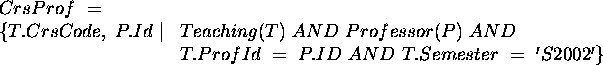
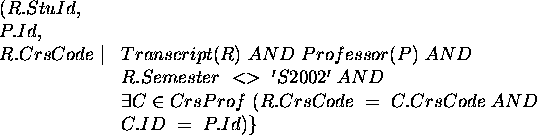
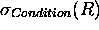 .
.
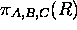 .
.
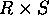 . (Assume R has
attributes A, B, C and S has attributes D and E.
. (Assume R has
attributes A, B, C and S has attributes D and E.
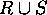 .
.