Relational Algebra
Tom Kelliher, CS 318
Feb. 11, 2002
Read 6.2--3.
E/R design example.
- Relational algebra's role.
- Primitive RA operators.
- Derived RA operators.
Queries and updates in SQL.
Query processing:
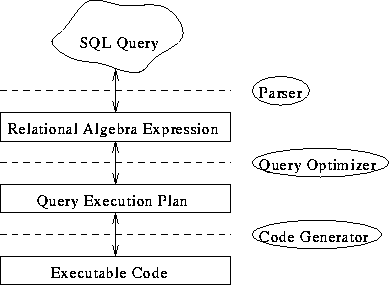
Generally, each operator takes:
- One or two relations.
- A conditional expression.
and produces a relation.
- Used to filter out tuples from a relation.
- Example:
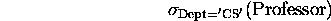
- General form:
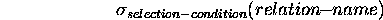
- Selection-condition can be extended with the usual boolean
operators.
- Only real restriction: Attributes named in the selection-condition
must belong to the relation.
- Used to filter out attributes from a relation.
- Example:
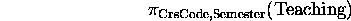
- Combination example:
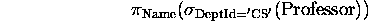
- Relations must be union-compatible:
- Same number of attributes.
- Attribute names are the same in both relations.
- Attribute domains match.
- Example:
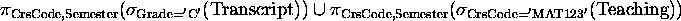
- Union-compatability required.
-
 : Everything in A and not in B.
: Everything in A and not in B.
Let  and
and  .
.  and
and  .
.
- Used to combine two relations. Expensive to compute.
-
 is the set of all tuples which can be formed by
combining a tuple of A with a tuple of B.
is the set of all tuples which can be formed by
combining a tuple of A with a tuple of B.
Let A be:
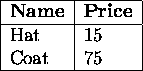
and B be:

 is:
is:
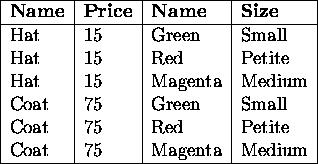
Whoops. To rename the attributes, we could write:
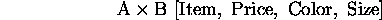
Assume we have the schemas Student and Transcript:

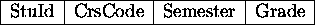
Write relational algebra expressions to determine the following:
- The names of all seniors.
- The name and address of the student whose Id is 123456789.
- The names of all juniors and those students who Id is between
111111111 and 222222222, inclusive.
- The names of all students who have taken CS318.
- The names of all sophomores who received A's during the F2001
semester.
- The names and Ids of any students who have never taken a course.
- Theta join:
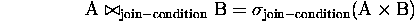
Example:
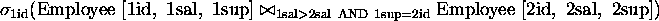
(Ids of all those who earn more than their supervisors.)
- Equijoin: only comparison operator is =.
Important because they ``reconstruct'' the database: Get names of all
students who have taken CS318.
- Natural join: equijoin on intersection of attributes where the
redundant attributes in each tuple are projected out.
- Let <s> and <t> be sets of attributes and let relation
 and relation
and relation  . Then:
. Then:
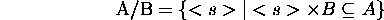
- Example. Let A be:

Let B be:

 .
.
- Derivation of division
 :
:

Thomas P. Kelliher
Thu Feb 7 19:14:59 EST 2002
Tom Kelliher


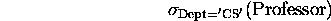
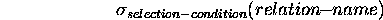
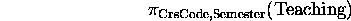
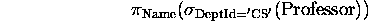
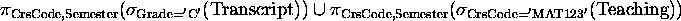
 : Everything in A and not in B.
: Everything in A and not in B.
 and
and  .
.  and
and  .
.
 is the set of all tuples which can be formed by
combining a tuple of A with a tuple of B.
is the set of all tuples which can be formed by
combining a tuple of A with a tuple of B.
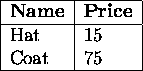

 is:
is:
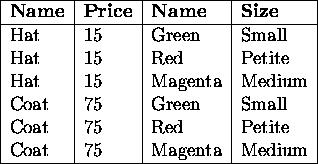
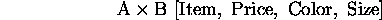

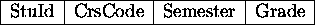
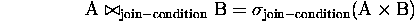
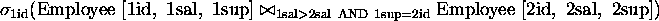
 and relation
and relation  . Then:
. Then:
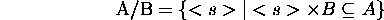


 .
.
 :
:
