Query Processing I
Tom Kelliher, CS 318
Apr. 22, 2002
Homework due Wednesday, start of class.
Read 13.4--7.
Indexing schemes.
- Introduction.
- Sorting.
- Computing projections.
-
SELECT processing.
Completion of query processing.
Given a table and one or more access paths, how do we structure queries to
optimize performance?
- Have to rely on external sorting techniques.
- Most important objective is to minimize disk I/O.
- In addition to the
SORT BY clause, sorting will be necessary
when DISTINCT is in use. Why?
- Assumptions: file consists of F pages and we have M memory
buffers at our disposal.
External sorting algorithm:
// Partial sort on runs of M pages.
do {
read next M pages from the file;
sort rows using an in-memory technique;
write the sorted M pages to a file of their own;
} until end of file;
// Merge the partial sorts into a final sorted file.
// Open files for reading to maintain a balanced tree organization
// of runs.
while there is more than one input run {
open M - 1 runs for reading
while there is a non-empty run {
choose the smallest tuple, with respect to sort key, from each
run;
output the smallest such tuple and delete it from its run;
}
write and close the output file;
}
}
M - 1 because we need one output buffer.
Rough example: file contains 13 pages, we have three buffers.
Questions:
- How many page accesses to obtain the partial sorts?
- How many page accesses to complete a merge step?
- How many merge steps?
- How many total page accesses to sort?
- Eliminating columns might result in duplicates.
DISTINCT clause.
- Eliminate duplicates by sorting or by hashing.
- Modifications to basic sort needed to support projections:
- Eliminate unnecessary columns from table when first reading pages
during the partial sort step.
- Eliminate duplicate rows while writing new files.
How will this running time compare to unadorned sort?
- Sketch of hashing:
- Need one input buffer, so we have M - 1 buffers available for
hashing.
- Find a hash function which hashes the projection columns onto the
buffers.
- Read file. For each row, gather projected columns and hash.
Flush each hash buffer to a file when full.
- For each hash file, read, sort, eliminate duplicates, write to
final output file.
Assuming a uniform distribution, each hash file will fit in the M
buffers. Quite a large file can be handled this way.
- Total number of page accesses?
- Union and set difference are similar.
Preliminaries:
- Our
SELECT model:
SELECT *
FROM R
WHERE Col1 op1 Val1 AND Col2 op2 VAL2 ... Coln opn Valn;
- Access path options when there is only one condition:
- No index --- scan the entire file.
Or, if file is sorted on Col1, perform a binary search to get
to the first ``qualifying'' tuple and then scan forward.
Cost?
-
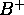 tree index on
tree index on Col1 --- Find first qualifying tuple
and then use sibling pointers to scan forward.
Cost? Suppose the file is unclustered? Sort the rids.
- Hash index on
Col1 --- Find bucket containing Val1
and scan.
Cost?
- Access path options when there are n conditions:
- No index --- scan the entire file.
Or, if file is sorted on several of the Coli, perform a binary
search to get to the first ``qualifying'' tuple and then scan forward.
Cost?
-
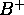 tree index on several columns.
tree index on several columns.
For this to be useful, a subset of the Coli must be a prefix of
the index columns. Example.
Cost?
- Hash index on several columns. All
opi must be equality.
The columns indexed on must be a subset of the Coli. Why?
Hash to find buckets, then check buckets for matches.
Cost?
Thomas P. Kelliher
Fri Apr 19 10:18:16 EDT 2002
Tom Kelliher
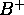 tree index on
tree index on 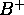 tree index on several columns.
tree index on several columns.