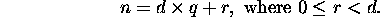
Tom Kelliher, MA 115
Oct. 17, 1997
Final: 9:00--11:00am on 12/15/97 in HS 149.
Read Section 3.6. Problems due Wed. 10/22: 3.3.31, 3.3.33, 3.3.38, 3.4.20, and 3.4.31.
For any integer n and any positive integer d, there exist unique integers q and r such that
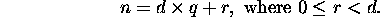
Examples:
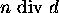 is the quotient of n divided by d.
is the quotient of n divided by d.
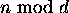 is the remainder of n divided by d.
is the remainder of n divided by d.
If 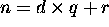 :
:
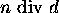 ?
?
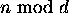 ?
?
Prove that any two consecutive integers have opposite parity.
Prove that the square of any odd integer can be written as 8m+1 for some integer m.
Prove that the product of any two consecutive integers is even. Two forks in the path: