The Coordinate Plane, Graphs & Graphing Calculators
Tom Kelliher, MA 114
Sept. 11, 1998
Announcements: Be sure to bring books, calculators. Homework questions?
From last time:
- Real numbers, solving quadratic equations.
Outline:
- The coordinate plane: distance, midpoint formulas, graphs of
equations.
- Graphs & graphing calculators: foibles and follies.
Assignment: Read 1.5--6.
- Cartesian (rectangular) coordinate system. Origin. X and Y axes.
Quadrants.
- The coordinates of a point are an ordered pair. Which order?
- Consider the points
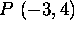 and
and 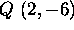 . What is the distance
between them?
. What is the distance
between them?
- The distance, D between two points
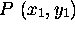 and
and 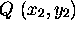 is:
is:
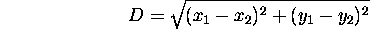
- Why? (Recall Pythagoras' theorem.)
- The midpoint of the line segment from
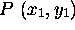 to
to 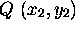 is:
is:
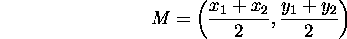
- Why? We must show that
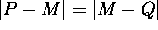 and
and 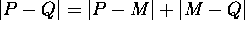 . Why is that sufficient?
. Why is that sufficient?
- Examples: 1.3.5, 7, 17.
- A graph of a function in two variables is the set of points whose
coordinates satisfy the equation.
- Consider the circle with center at
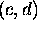 and radius r. Using
the distance formula, derive its equation:
and radius r. Using
the distance formula, derive its equation: 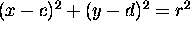 .
.
- What's the equation for the circle of radius 5 centered at the
origin?
- By completing the squares, find the center and radius of this circle:
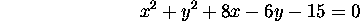
- Examples: 1.1.19, 23, 29.
- Viewing windows: Seeing too much, seeing too little.
- Try the exploration on Pg. 35.
- Experiment: Set your calculator's window to Xmin = 0, Xmax = 3, Ymin
= -4, Ymax = 0. Then, graph
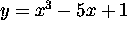 . Just looking at the graph,
what type of a curve do you think it is? Set the zoom to Zstandard and
check your guess.
. Just looking at the graph,
what type of a curve do you think it is? Set the zoom to Zstandard and
check your guess.
- Observations?
- Aspect ratio --- making circles look like circles. Using Zstandard,
graph the upper half of the circle centered at the origin of radius 4:
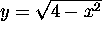 . The circle isn't circular. Why? How do we fix it? Use
Zsquare. Now, the curve doesn't touch the X-axis. Move the cursor to X =
1.9, Y = .1 and zoom in. Does the curve touch the axis now? Why not?
. The circle isn't circular. Why? How do we fix it? Use
Zsquare. Now, the curve doesn't touch the X-axis. Move the cursor to X =
1.9, Y = .1 and zoom in. Does the curve touch the axis now? Why not?
- How does the calculator graph? Starting from window size, pixels in
display, and equation.
- Digitizing and aliasing --- Using Zstandard, graph
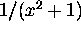 . This
function is defined for every value of x and only asymptotically approaches
0, but they all aren't graphed. Why?
. This
function is defined for every value of x and only asymptotically approaches
0, but they all aren't graphed. Why?
- Complete graphs: characterize the behavior of the equation.
Examples: parabola, sine wave. Important to zoom in, out, and around to be
sure you have the complete behavior.
- Be sure to read Graphing Convention on pg. 45.
- Examples: 1.4.18, 19.
Thomas P. Kelliher
Thu Sep 10 11:19:24 EDT 1998
Tom Kelliher
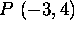 and
and 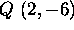 . What is the distance
between them?
. What is the distance
between them?
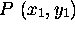 and
and 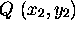 is:
is:
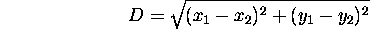
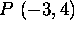 and
and 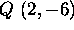 . What is the distance
between them?
. What is the distance
between them?
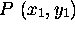 and
and 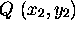 is:
is:
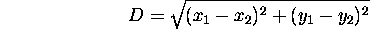
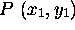 to
to 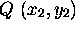 is:
is:
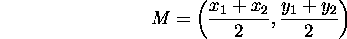
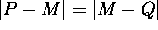 and
and 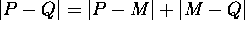 . Why is that sufficient?
. Why is that sufficient?
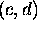 and radius r. Using
the distance formula, derive its equation:
and radius r. Using
the distance formula, derive its equation: 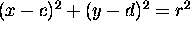 .
.
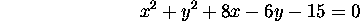
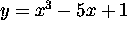 . Just looking at the graph,
what type of a curve do you think it is? Set the zoom to Zstandard and
check your guess.
. Just looking at the graph,
what type of a curve do you think it is? Set the zoom to Zstandard and
check your guess.
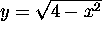 . The circle isn't circular. Why? How do we fix it? Use
Zsquare. Now, the curve doesn't touch the X-axis. Move the cursor to X =
1.9, Y = .1 and zoom in. Does the curve touch the axis now? Why not?
. The circle isn't circular. Why? How do we fix it? Use
Zsquare. Now, the curve doesn't touch the X-axis. Move the cursor to X =
1.9, Y = .1 and zoom in. Does the curve touch the axis now? Why not?
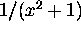 . This
function is defined for every value of x and only asymptotically approaches
0, but they all aren't graphed. Why?
. This
function is defined for every value of x and only asymptotically approaches
0, but they all aren't graphed. Why?