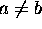 , then
, then
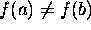 .
.
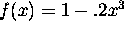 . Zoom or trace to make sure.) If a function passes the
horizontal line test, then it is one-to-one.
. Zoom or trace to make sure.) If a function passes the
horizontal line test, then it is one-to-one.
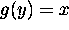 exactly when
exactly when 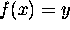 .
.
Do 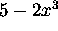 and
and 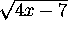 have inverses? If so, find them
algebraically.
have inverses? If so, find them
algebraically.
Tom Kelliher, MA 114
Oct. 27, 1998
Collect homework. Questions on homework? Exam next Friday. Trig.\ situation.
Read 3.1. Problems due Monday from 2.7: 4, 6, 16, 26, 36, 42.
Definitions:
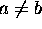 , then
, then
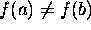 .
.
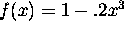 . Zoom or trace to make sure.) If a function passes the
horizontal line test, then it is one-to-one.
. Zoom or trace to make sure.) If a function passes the
horizontal line test, then it is one-to-one.
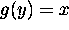 exactly when
exactly when 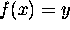 .
.

Do 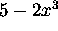 and
and 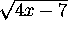 have inverses? If so, find them
algebraically.
have inverses? If so, find them
algebraically.
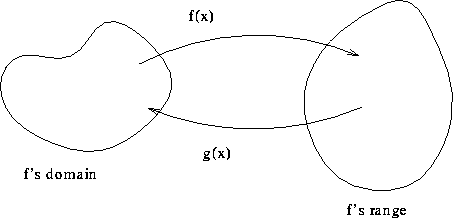
Suppose f and g are functions such that
Then f is one-to-one and its inverse is g.
Show that 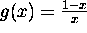 is the inverse of
is the inverse of 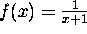 .
.
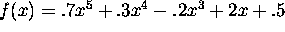 have an inverse?
have an inverse?
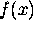 ? What do we have if
we swap the two equations?
? What do we have if
we swap the two equations?
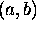 is on the graph of f exactly when b,a is on
the graph of f's inverse.
is on the graph of f exactly when b,a is on
the graph of f's inverse.
Often, the inverse of 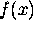 is denoted
is denoted 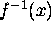 . This is not
division.
. This is not
division.
If there's time, look at some of the word problems on pg. 147.