Security Models
Tom Kelliher, CS 325
Oct. 31, 2011
Status reports due.
Read 5.4.
Trust and security policies.
- Modeling multiple levels of security.
- Modeling theoretical limitations of security systems
Trusted operating system design.
That is, the military model.
A lattice defines a partial order on a set using a user-defined 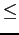 operator. The operator must satisfy two properties over the set:
operator. The operator must satisfy two properties over the set:
- Transitive: If
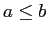 and
and 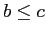 then
then 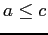 .
.
- Antisymmetric: If
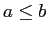 and
and 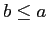 then
then  .
.
A bounded lattice has a top and bottom:
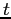 is the top if
is the top if 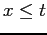 for all
for all 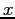 in
in  .
.
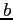 is the bottom if
is the bottom if 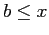 for all
for all 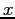 in
in  .
.
Examples:
- The power set of
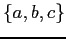 under the operation ``is a subset of.''
under the operation ``is a subset of.''
Is it bounded?
- The natural numbers under the mathematical operation
 .
.
Is it bounded? Isn't it a total order?
- Goal is to describe secure information flows and acceptable information
flows between subjects and objects.
- Subjects may have read or write access to objects.
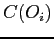 denotes the classification of
denotes the classification of 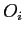 .
.
Similarly, 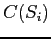 denotes the clearance of
denotes the clearance of 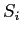 .
.
Suppose:
- What objects can
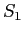 be allowed to read?
be allowed to read? 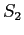 ?
?
- If
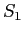 has read access to
has read access to 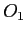 , can it be granted write access to
, can it be granted write access to 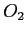 ?
?
Necessary properties for ensuring confidentiality:
- Simple security property:
 may read
may read  only if
only if
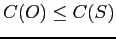 .
.
- *-Property: If
 has read access to
has read access to 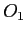 , it may be granted write access
to
, it may be granted write access
to 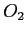 only if
only if
 .
.
Information should only flow from less secure objects to more secure
objects.
Biba's integrity model is similar -- non-trusted information should not
influence trusted information.
- Is security configuration X attainable?
- Given security configuration Y, can subject S gain access to object
O?
- Trivial example.
Suppose 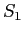 has a transferable read right on
has a transferable read right on 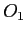 .
.
Can 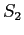 gain access to
gain access to 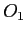 ? Will it?
? Will it?
Model consists of subjects, objects, an access control matrix (all subjects
are also treated as objects, to implement the ``control'' right), and a set
of rights.
Two special rights: own (on objects) and control (on subjects)
Operations:
- Create object; create subject. Creating subject owns or controls,
respectively.
- Delete object; delete subject. Deleting subject must own or control,
respectively.
- Read access right R of S on O. Subject must control S or own O.
- Grant right R to S on O. Subject must own O.
- Delete right R of S on O. Subject must own O or control S.
- Transfer right R to S on O. Subject must have R* (transferable version
of R) on O.
Graham-Denning is a general access control model.
Harrison-Ruzzo-Ullman generalizes Graham-Denning to ask if certain
situations are obtainable.
Take-Grant Systems are yet another model.
Thomas P. Kelliher
2011-10-30
Tom Kelliher
![]() operator. The operator must satisfy two properties over the set:
operator. The operator must satisfy two properties over the set:
![]() denotes the clearance of
denotes the clearance of ![]() .
.
![]() has a transferable read right on
has a transferable read right on ![]() .
.
![]() gain access to
gain access to ![]() ? Will it?
? Will it?