Floating Point Representation
Tom Kelliher, CS 220
Nov. 4, 2011
Milestone due.
Read 4.1-4.3 for Wednesday.
Binary addition, subtraction, multiplication.
- Floating point numbers.
- Floating point representation.
- Floating point addition.
Project day, then introduction to building a simple MIPS datapath.
- Do we really need a way to represent floating point numbers?
- Recall:
where mantissa is normalized:
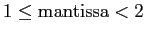 .
.
Note: mantissa is sign-magnitude notation, while exponent is 2's
complement!
- This has to fit into one word. What are the tradeoffs?
Is there a way to increase the range, while keeping the same precision?
(Hint: consider changing the base of the exponent.)
- Finally, we would like to compare floating point numbers using
integer compare hardware. How should we order the fields of the floating
point representation in order to achieve this?
What problem will we run into, and how do we solve it?
- Underflow and overflow.
- Formats:
- Single precision: 23 bit mantissa, eight bit exponent.
- Double precision: 52 bit mantissa, 11 bit exponent.
- Some real problems:
- Accumulated errors in extended computations.
Rounding techniques, in conjunction with guard, round, and sticky bits
help with this.
- Hardware that doesn't do floating point divide.
- Getting floating point right is hard. (Ask Intel.)
Doing it right and fast is even harder.
Fields of a single precision floating point number:
- Mantissa sign.
- Exponent: Bias 127, 8 bits.
How to use the bias:
-
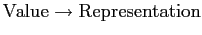 : Add the bias.
: Add the bias.
-
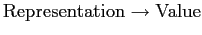 : Subtract the bias.
: Subtract the bias.
- Mantissa magnitude, 23 bits. Normalized.
Additional Feature: The hidden bit.
Values (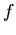 is the fractional part of the mantissa):
is the fractional part of the mantissa):
- V = NaN, if
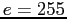 and
and 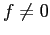 .
.
- V =
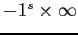 , if
, if 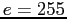 and
and 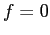 .
.
- V =
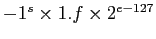 , if
, if 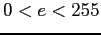 .
.
- V =
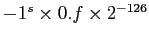 , if
, if  and
and 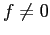 . (Denormalized.)
. (Denormalized.)
- V =
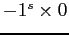 , if
, if  and
and 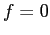 .
.
Examples:
- Represent the value 3.14159E8 in IEEE FP. (In integer hex, it's 0x12B9AF98.)
FYI, here's a C program to confirm the result:
#include <stdio.h>
int main()
{
float x = 3.14159E8;
int *ptr = (int *) &x;
printf("%E %X\n", x, *ptr);
return 0;
}
- What is the value of the FP representation 0XC1320000?
- How do we do this with pencil and paper?
Add decimal 9.567E3 and 5.678E2.
- What is the algorithm?
- FP hardware:
Explain all the blocks, particularly the muxes!
Thomas P. Kelliher
2011-11-03
Tom Kelliher
![\begin{figure}\centering\includegraphics[width=5in]{Figures/fltPtAdd.eps}\end{figure}](nov04img15.png)