Operations, Operands, and Instructions
Tom Kelliher, CS 220
Sept. 14, 2009
Read 2.6-2.7.
Macro-architectural trends; IC fab.
- Introduction.
- Simple arithmetic operations
- Operands: registers, memory.
- R-Format and I-Format instruction formats.
Logical and conditional instructions in MIPS.
- Stored program concept. Is it data, address of data, instruction, or
what?
- Instruction set.
- Operands.
- Collected design principles:
- Simplicity favors regularity. A simple architecture will
result in regular, clean implementations.
Example: arithmetic operations that have two source operands.
- Smaller is faster. Storage capacity vs. speed tradeoffs.
Examples: Register file size. Word size. Instruction set cardinality.
- Make the common case fast.
Example: The most common immediate values are small. Store them in the
instruction.
- Good design demands good compromises. We can't optimize
everything.
Example: Having only a few instruction formats, all of which are
regular.
Instruction semantics:
add a, b, c # This, BTW, is a comment.
sub a, a, b
De-compile into a single HLL statement:
add a, b, c
add a, a, d
add a, a, e
Compile each of the following:
a = b + c;
d = a - e;
f = (g + h) - (i + j);
Where are the operands?
$0 to $31 or $s0, $t0, etc.
Example:
add $1, $2, $3
Properties of registers:
- Number of registers. 32 for MIPS, including the hardwired register.
Two ways of naming: numbers, convention ``nicknames''. Why not more? Size
of register file, size of operand fields within instructions.
- Number of bits/register. 32. Word size.
32 bits is 4 bytes.
Implications: size of address space, datapath width.
- General purpose vs. special purpose.
MIPS, M68000, x86.
- HLL have complex data structures such as arrays and structs. How are they
handled?
- Data transfer instructions: load, store. operands: memory address,
register.
- Actual MIPS instructions: lw, sw.
Base and offset addressing: lw $s0, 8($s1)
- MIPS memory is byte addressable, so word addresses differ by 4:
Alignment restriction -- Word addresses start on word boundaries. A good
compromise.
This isn't the only way to number the bytes within word. ``Big endian.''
Base, offset addressing. Usefulness when accessing a member of an object.
Compile each of the following:
A[12] = h + A[8];
A[j] = h + A[i];
where h is in $1, i is in $2, j is in
$3, and the base address of A, an int array of 100
words, is in $4.
Variables in registers are simpler to use and faster than variables
in memory. Compilers must be clever in optimizing register use.
Example:
lw $1, 4($0)
lw $2, 8($0)
add $1, $1, $2
sw $1 0($0)
Explain what this is doing, in plain English.
Another example:
lw $t0, 0($s0)
addi $s0, $s0, 4
lw $t1, 0($s0)
add $t0, $t0, $t1
addi $s0, $s0, 4
sw $t0, 0($s0)
Again, explain.
Basics:
- Conventional number systems are weighted and positional.
- A base
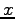 systems uses
systems uses 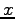 numerals (symbols).
numerals (symbols).
- Representing negative values is tricky -- we cheat in decimal.
- The hexadecimal system and its relationship to binary.
- Base conversions.
- msb and lsb.
- Consider a four bit unsigned binary integer:
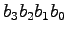 . What
does
. What
does 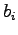 contribute to the value of the number?
contribute to the value of the number?
- What range of values can be represented using just four bits? Eight
bits?
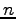 bits?
bits?
How might we designate that a binary number is negative?
Two problems with this approach:
- Two representations for zero.
- Adder design becomes more difficult.
This is sign-magnitude representation.
Again, msb is sign bit.
- Positive values have same representation as for unsigned case.
- To compute the inverse, complement all the bits and add 1.
- One 0.
- Asymmetric range: one more negative value.
- Negation:
- Two's complement is called by that name because
Which is okay because 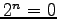 . Wait -- Why?
. Wait -- Why?
Obviously,
So:
Hence our algorithm for negating a two's complement number.
- Sign Extension:
- How do you place a 16-bit signed immediate into a
register?
- How do you load a signed byte into register?
- The sign extension algorithm.
- Load byte unsigned.
- How can this simple procedure preserve the value of a negative
number? Proof?
- Signed & unsigned comparison. Or, sometimes 1111 is less than 0000
and sometimes it's not.
Example instruction: add $s2, $s0, $s1
Fields:
- Op: Opcode.
- Rs: First source operand.
- Rt: Second source operand.
- Rd: Destination operand.
- Shamt: Shift amount -- ignore for now.
- Func: Function. Further specification of the opcode.
In assembly: Op/Func Rd, Rs, Rt
Notes:
- Become familiar with field positions and sizes for all three
formats.
- Example encodings:
| Assembly |
Op |
Rs |
Rt |
Rd |
Shamt |
Func |
add $1, $2, $3 |
0 |
2 |
3 |
1 |
D.C. |
32 |
sub $4, $5, $6 |
0 |
5 |
6 |
4 |
D.C. |
34 |
Example instruction: lw $s0 8($s1)
Fields:
- Op: Opcode.
- Rs: Source register.
- Rt: Destination register.
- Address: 16-bit signed immediate value.
Offset range?
Example encoding of:
A[20] += 72;
| Assembly |
Op |
Rs |
Rt |
Immediate |
lw $t1, 80($s0) |
35 |
16 |
9 |
80 |
addi $t2, $t1, 72 |
8 |
9 |
10 |
72 |
sw $t2, 80($s0) |
43 |
16 |
10 |
80 |
Thomas P. Kelliher
2009-09-13
Tom Kelliher
![\begin{figure}\centering\includegraphics[]{Figures/memoryMap.eps}\end{figure}](sep14img1.png)
![\begin{figure}\centering\includegraphics[]{Figures/memoryMap.eps}\end{figure}](sep14img1.png)
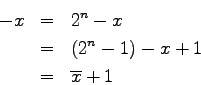
![\begin{figure}\centering\includegraphics[]{Figures/rFormat.eps}\end{figure}](sep14img10.png)
![\begin{figure}\centering\includegraphics[]{Figures/iFormat.eps}\end{figure}](sep14img11.png)