Toolkit Functions I
Tom Kelliher, MA 114
Sept. 26, 2001
No new reading, but another online quiz on 2.3.
Characteristics of functions.
Keys to understanding toolkit functions:
- Behavior around the origin.
- Above/below line y = x.
- Symmetry: even/odd.
- Asymptotes.
Functions and terminology:
- Constant function.
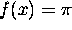 .
.
- Linear function.
Identity function.
- Quadratic function.
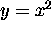
Parabola. Concave up. Even symmetry. Vertex --- turning point.
- Cubic function.
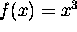
Steeper slope than quadratic. Odd symmetry. Concave up and down.
- Square root function.
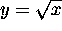 Equivalent to
Equivalent to 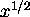 .
.
Calculator warning: Use parentheses --- 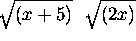 .
.
Principal (positive) square root --- otherwise, no function. But, we
must remember when we have 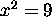 that
that 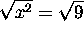 ,
, 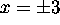 .
.
Concave down.
- Exponential function.
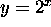
Concave up. Horizontal asymptote at y = 0.
- Reciprocal function.
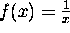 Equivalent to
Equivalent to 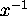 .
.
Vertical asymptote at x = 0. Odd symmetry. Also has horizontal asymptote
at y = 0.
- Sine function
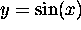
Period is 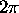 . Turning points at
. Turning points at 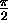 ,
, 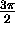 ,
etc. Zeroes at 0,
,
etc. Zeroes at 0, 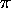 ,
, 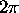 , etc.
, etc.
- Absolute value function
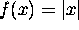
Finding the ABS key on the calculator --- three keys below
2nd key. Example of a piecewise-defined function:
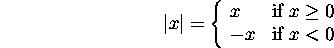
(How do I read one of these things???)
Use your calculator to graph each of the toolkit functions, using a window
of 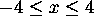 and
and 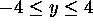 . For each function, answer
these questions:
. For each function, answer
these questions:
- Identify the domain and range of the function.
- For what part of the domain is the function above the line y = x?
below?
- What symmetry does the function have, if any? What are its
asymptotes, if any?
Pg. 69: 1, 3.
Thomas P. Kelliher
Mon Sep 24 09:37:42 EDT 2001
Tom Kelliher
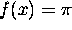 .
.
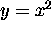
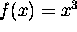
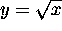 Equivalent to
Equivalent to 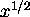 .
.
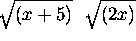 .
.
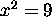 that
that 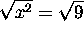 ,
, 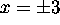 .
.
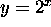
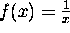 Equivalent to
Equivalent to 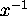 .
.
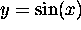
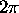 . Turning points at
. Turning points at 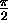 ,
, 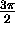 ,
etc. Zeroes at 0,
,
etc. Zeroes at 0, 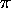 ,
, 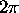 , etc.
, etc.
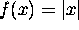
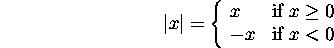
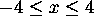 and
and 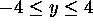 . For each function, answer
these questions:
. For each function, answer
these questions: