2-D Transformations
Tom Kelliher, CS 320
Feb. 23, 1998
Announcements: Homework due tonight.
From last time:
- Pong.
Outline:
- Idea.
- Preliminaries.
- Transformations.
Assignment: Read Chapter 5.
Three primitive transformation:
- Rotation.
- Scaling.
- Translation.
We'll consider each in turn.
The idea is to perform all transformations via matrix multiplications:
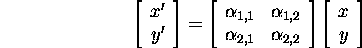
I'll assume you're familiar with (from 5.1):
- Vector spaces and their properties.
- Dot product.
- The vector 2-norm:
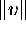 .
.
- Angle between two vectors:

- Properties of matrices.
- Some trigonometry.
We're all probably somewhat rusty. I know I am.
Consider rotating the point 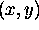 by
by 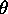 about the origin.
about the origin.

With a little magic:

What's our transformation matrix look like?
- ``Contract'' or ``expand'' a point (polygon).
- Point moves in relation to origin.
- Differential, uniform scalings.

Matrix representation?
Move the point:

Matrix representation?
- Use allows use to achieve translations via matrix multiplications.
- Add a third coordinate to a point:
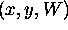 .
.
- Two sets of homogeneous coordinates represent the same point iff they
are multiples of each other.
- A ``homogenized'' point.
Our translation:
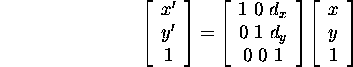
Can we combine transformations?
- Consider composing two translations:
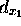 ,
, 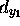 and
and
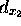 ,
, 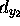 .
.
- Consider two scalings.
- Consider two rotations.
- Rigid body. Arbitrary sequence of translations and rotations.
- Affine. Parallelism of lines preserved, but not lengths nor angles.
- Shear (affine).
Consider the x-shear transformation:

What's the y-shear transformation matrix look like?
- How do we rotate about an arbitrary point?
- How do we scale about an arbitrary point?
Thomas P. Kelliher
Sun Feb 22 21:58:29 EST 1998
Tom Kelliher
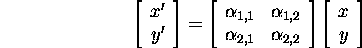
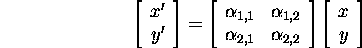
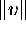 .
.

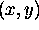 by
by 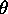 about the origin.
about the origin.




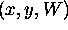 .
.
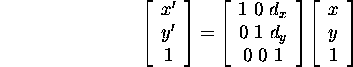
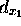 ,
, 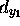 and
and
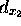 ,
, 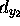 .
.
