Introduction to OpenGL

Tom Kelliher, CS 320

Feb. 2, 1998

Announcements:

From last time:

1. Programmer's interface.

2. Pictorial history of computer graphics.

3. Modeling-Rendering paradigm.

4. Graphics architectures.

Outline:

1. Introduction: Sierpinski gasket, pen-plotter model, vertex specification, coordinate systems.

2. OpenGL API.

3. Primitive basics: points, line segments, polygons.

Assignment: Browse the on-line resources and the man pages on phoenix. In particular, look at the OpenGL Programming Guide .

Introduction

Consider the Sierpinski gasket problem for a triangle:

// Initialize.
clear the viewing window;
set vertices of the triangle;
let currentPoint = random point in interior of triangle;
randomly select one of the three triangle vertices;

// Run.
while (notDone)
{
   nextPoint = point half-way between currentPoint and
      selected vertex;

   display nextPoint;

   currentPoint = nextPoint;
   randomly select one of the three triangle vertices;
}

1. In what coordinate system do we work?

2. In how many dimensions?

The Pen-Plotter Model

Note that all our output devices are 2-D.

1. Uses a gantry to move a pen.

2. Gantry moves in x and y.

3. Pen can be raised and lowered.

4. Operations:
   1. moveto(x, y);

   2. lineto(x, y);

5. This model is still in use with pen-plotters and PDLs such as Postscript.

6. How do we extend to 3-D?
   1. Must compute the 2-D projection of 3-D points. (Application of trigonometry, which you should review for later.)

   2. Should application or API perform the projections?

7. We can set z=0 so that we're working 2-D in 3-D.

Vertex Specification in OpenGL

Can't do much without vertices.

Indicator for the general form: glVertex*() (see man page on phoenix for glvertex .

Some examples:

1. glVertex2i(GLint xi, GLint yi);

2. glVertex3f(GLfloat x, GLfloat y);

3. Using an array to store the vertex coordinates:

   GLfloat vertex[3] = { 0.0f, 1.0f, 2.0f };
   
   glVertex3fv(vertex);
   

Vertices are grouped using glBegin()/glEnd():

glBegin(GL_LINES);
   glVertex2f(x1, y1);
   glVertex2f(x2, y2);
   glVertex2f(x3, y3);
   glVertex2f(x4, y4);
glEnd();

glBegin(GL_POINTS);
   glVertex2f(x1, y1);
   glVertex2f(x2, y2);
   glVertex2f(x3, y3);
   glVertex2f(x4, y4);
glEnd();

Heart of the Sierpinski gasket program:

void display(void)
{
   static point2 p = { x, y }; /* Initial point.
   int i;

   i = rand() % 3;

   p[0] = (p[0] + triangle[0]) / 2.0;
   p[1] = (p[1] + triangle[1]) / 2.0;

   glBegin(GL_POINTS);
      glVertex2fv(p);
   glEnd();
}

Coordinate Systems

What are our units for x, y, and z?

1. Originally, graphics systems worked in coordinates of display device.

2. Portability?

3. Much more convenient to work in problem coordinates, let API convert: device independence.

4. Mapping from world coordinates to device coordinates. For us, window coordinates.

OpenGL API

Support provided by a graphics API:

1. Primitive functions: points, line segments, polygons, text, curves, surfaces.

2. Attribute functions: color, fill, type face.

3. Viewing functions: attributes of the synthetic camera.

4. Transformation functions: rotation, translation, scaling. Matrix computations.

5. Input functions: keyboard, pointing device.

6. System communication: window system, OS, other workstations, other users.

OpenGL Library Organization:

Primitive Basics

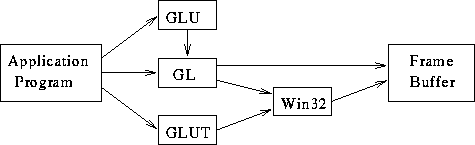
Consider:

glBegin(primitiveType)
   glVertex*( ... );
   // ...
   glVertex*( ... );
glEnd();

1. GL_POINTS .

2. GL_LINES .

3. GL_LINE_STRIP .

4. GL_LINE_LOOP . When is this not a polygon?

Polygon Basics

1. Polygons have interiors which can be filled.

2. What is filling? Color, pattern (bitmap) fills.

3. Simple polygon: no edges cross.

4. When filling, how do we determine if a point is interior? Crossing test.

5. Fill example: five-pointed star. Scanlines. Is this the effect we want?

6. Winding test improvement:
   1. Pick any vertex and direction.

   2. Traverse the polygon, labeling each edge with direction of traversal.

   3. Scanline crosses ``up'' edge: add 1. Crosses ``down'' edge: subtract 1.

   4. Point's winding number starts at 0. In interior if final winding number not 0.

7. Complications: lines parallel to scanline, intersections with vertices.

8. Convex and concave polygons.
   1. Definitions.

   2. Concave polygons can present problems.

   3. Often, hardware and software supports triangles.

   4. 2-D polygon convexity test: for any interior point, it is ``to the right'' when traversing the edges clockwise.