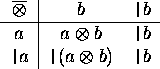Special Cases of Parallel Prefix Networks
Tom Kelliher, CS 315
Mar. 29, 1999
Read 1.2.3, 1.2.4.
Parallel prefix on a 2-D array.
- Parallel prefix on arbitrary networks.
- Parallel segmented prefix computations.
Carry save, multiplication, convolution.
Consider an arbitrary graph/network:
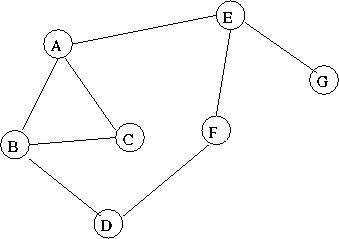
Form the breadth-first spanning tree from vertex A.
Properties of the breadth-first spanning tree:
- Finds shortest path from distinguished vertex to all other vertices.
- Depth is at most diameter of graph. (Find an example where the depth
is less than the diameter of the graph.)
- Not necessarily binary.
Observation: parallel prefix algorithm can be implemented with slowdown at
most the diameter of the graph.
Idea: each vertex of the network simulates a leaf and an internal vertex of
the tree.
- Draw for example graph.
- Do an example.
Definition:
A sequence of prefix computations that use the same associative operator
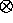 , but on disjoint sets of data.
, but on disjoint sets of data.
Example: Addition on 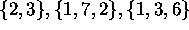 .
.
- Obviously, we can solve using three prefix computations. With a
trick, we can do it in one.
- The trick: use
| as a barrier symbol at the start of each set
of data.
- The data set:
|2, 3, |1, 7, 2, |1, 3, 6.
Redefine our operator:
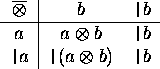
``Forget about everything to the left of the barrier.''
- Run the example.
- What is the running time of the parallel segmented prefix
computation?
Thomas P. Kelliher
Mon Mar 29 10:41:52 EST 1999
Tom Kelliher


, but on disjoint sets of data.
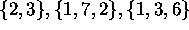 .
.