Algorithm Assessment and Simulating Large Machines
Tom Kelliher, CS 315
Jan. 29, 1999
Sorting on a linear array, algorithm assessment.
- Algorithm assessment.
- Simulating larger machines.
- Examples.
Bit models, lower bounds.
How can we measure a parallel algorithm? Apply following to sorting on the
linear array.
- Run time: T.
- Number of processors: N.
- Speedup: Let
 be the running time of the fastest sequential
algorithm. Then:
be the running time of the fastest sequential
algorithm. Then:

What is linear speedup?
Say you have P processors. Speedup is at most P. Why? (Hint: a
parallel algorithm that runs in T steps on P processors can be
simulated on a sequential machine in how many steps?)
- Work: W = TP.
Measures algorithm inefficiencies due to idle processors.
- Efficiency of processor utilization:
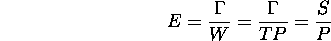
- Is it always possible to minimize T and E?
Example: consider two algorithms for solving a problem of size M:
- M steps on an M processor machine.
-
 steps on an
steps on an  processor machine.
processor machine.
If we have an  processor machine and need to run the algorithm X
times, which algorithm should we use? Assume the
processor machine and need to run the algorithm X
times, which algorithm should we use? Assume the  processor machine
may be split in M M processor machines.
processor machine
may be split in M M processor machines.
(Recall:  .)
.)
Let's say we want to solve a problem of size N with P processors.
- We generally assume that P = N. Is this valid? --- More later.
- Suppose, we have
 fine-grain processors in a
linear array. Can we sort N numbers?
fine-grain processors in a
linear array. Can we sort N numbers?
Fine-grain vs. coarse-grain processing.
- Assuming appropriate granularity, here's how we simulate 12
processors on 3 processors:

What about simulating  processors on
processors on  processors, where
processors, where  ?
?
What slowdown do we encounter?
- Is the scaled-down algorithm less efficient?
- So, why do we assume, in general, that P = N?
Implications:
- Given an algorithm efficient for large P, we can construct one
efficient for small P.
- What about the converse?
- 1.2
-
Consider two algorithms for solving a a problem of size M, one that runs
in M steps on an M-processor machine and one that runs in
 steps on an
steps on an  -processor machine. Which algorithm is more
efficient?
-processor machine. Which algorithm is more
efficient?
Assume that the cost of running a P-processor machine for T steps is
 , where
, where  and
and  are constants and P = M or
are constants and P = M or
 . For what values of
. For what values of  and
and  is the first algorithm
cheaper to run? For what values of
is the first algorithm
cheaper to run? For what values of  and
and  is the second
algorithm cheaper to run?
is the second
algorithm cheaper to run?
- 1.3
-
Consider two algorithms for solving a problem of size M, one that runs in
M steps on an M-processor machine and one that runs in
 steps
on an
steps
on an  -processor machine. Which algorithm will run faster on an
N-processor machine? (Hint: Your answer depends on the relative sizes of
M and N, and you will need to use the fact that an N-processor
machine can simulate a P-processor machine with slowdown
-processor machine. Which algorithm will run faster on an
N-processor machine? (Hint: Your answer depends on the relative sizes of
M and N, and you will need to use the fact that an N-processor
machine can simulate a P-processor machine with slowdown  .)
.)
Thomas P. Kelliher
Fri Jan 29 10:40:33 EST 1999
Tom Kelliher
 be the running time of the fastest sequential
algorithm. Then:
be the running time of the fastest sequential
algorithm. Then:

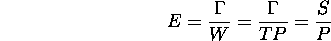
 steps on an
steps on an  processor machine.
processor machine.
 processor machine and need to run the algorithm X
times, which algorithm should we use? Assume the
processor machine and need to run the algorithm X
times, which algorithm should we use? Assume the  processor machine
may be split in M M processor machines.
processor machine
may be split in M M processor machines.
 .)
.)
 fine-grain processors in a
linear array. Can we sort N numbers?
fine-grain processors in a
linear array. Can we sort N numbers?

 processors on
processors on  processors, where
processors, where  ?
?
 steps on an
steps on an  -processor machine. Which algorithm is more
efficient?
-processor machine. Which algorithm is more
efficient?
 , where
, where  and
and  are constants and P = M or
are constants and P = M or
 . For what values of
. For what values of  and
and  is the first algorithm
cheaper to run? For what values of
is the first algorithm
cheaper to run? For what values of  and
and  is the second
algorithm cheaper to run?
is the second
algorithm cheaper to run?
 steps
on an
steps
on an  -processor machine. Which algorithm will run faster on an
N-processor machine? (Hint: Your answer depends on the relative sizes of
M and N, and you will need to use the fact that an N-processor
machine can simulate a P-processor machine with slowdown
-processor machine. Which algorithm will run faster on an
N-processor machine? (Hint: Your answer depends on the relative sizes of
M and N, and you will need to use the fact that an N-processor
machine can simulate a P-processor machine with slowdown  .)
.)