Foundations & Sorting on a Linear Array
Tom Kelliher, CS 315
Jan. 22, 1999
- Introduction.
- No credit review quiz.
- Foundations: asymptotic analysis, mathematical induction, loop
invariants.
- Sorting on a linear array: linear arrays, sorting, time analysis
Continue reading Section 1.1.
Algorithm evaluation.
Define: O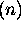 ,
, 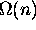 ,
, 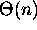 , o
, o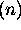 , and
, and 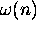 , using
, using
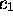 ,
, 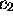 , and
, and 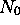 .
.
Notes:
- Throw out constants and lower order terms.
- Meaning/use of
 and
and 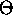 .
.
Prove that a complete binary tree of height h has 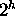 leaves.
leaves.
Basis, inductive hypothesis, inductive step.
Four characteristics:
- Must be true upon entry into the loop
- Execution of the loop body must preserve the invariant
- Invariant must capture the correctness and the meaning of the
loop
- Loop must terminate
Consider the following sorting algorithm which sorts the n elements
of data (the elements are indexed 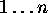 ):
):
for i := n downto 2 do
largest := i;
for j := i-1 downto 1 do
if data[j] > data[largest]
largest := j;
swap(data[largest], data[i]);
Prove that the algorithm sorts the elements of the array data into
ascending order.
First, demonstrate the algorithm on the array
int data[] = { 12, 19, 6, 15 };
A linear array:

Cell properties:
- Local program: a ``few'' operations.
- Local storage: a ``few'' words of data.
- Operation sequence:
- Receive inputs from neighbors.
- Read local storage.
- Perform computation indicated by local program.
- Generate output for neighbors.
- Update local storage.
- Synchronized to a global clock.
- Must all the programs be identical? Elegance?
Communication properties:
- Bidirectional links between cells.
- Left, right neighbors.
- Fixed connection network.
- Data pulsing through network: systolic computation.
- Phase 1: sorting program.
- Accept input from left neighbor.
- Compare to stored value.
- Output larger value to right neighbor.
- Store smaller value.
- Phase 2: output. Begin passing left when no more input is received
from the left neighbor.
Example: sort 12, 19, 6, 15.
How many steps to sort? How many steps to output?
Thomas P. Kelliher
Fri Jan 22 09:23:26 EST 1999
Tom Kelliher
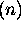 ,
, 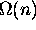 ,
, 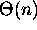 , o
, o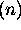 , and
, and 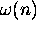 , using
, using
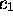 ,
, 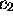 , and
, and 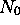 .
.
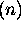 ,
, 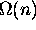 ,
, 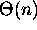 , o
, o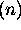 , and
, and 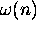 , using
, using
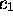 ,
, 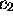 , and
, and 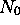 .
.
 and
and 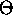 .
.
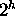 leaves.
leaves.
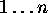 ):
):
