Carry Lookahead Addition

Tom Kelliher, CS 315

Feb. 26, 1999

Administrivia

Announcements

Homework due Monday.

Assignment

Read 1.2.2.

From Last Time

Summary of fixed-connection network model.

Outline

1. Carry lookahead addition algorithm, proof.

Coming Up

Parallel prefix computations.

Carry Lookahead Addition

1. In general, the sum of two n-bit numbers results in an n+1-bit sum.

2. The problem reduces to computing the carries.

3. For each bit position we determine if it would
   1. Propagate a carry (p).

   2. Generate a carry (g).

   3. Stop a carry (s).

   What's the ``truth table'' for this.

4. Example: 0x5c92 and 0x685c.

5. The computation is carried out in a binary tree with addend, augend bits transmitted to the leaves.

   Dimensions of the tree?

6. Steps of the computations:
   1. Step 1: compute p, g, s in the leaves.

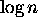   2. ascending steps:
      1. Receive inputs from children, who ``erase'' their values.

      2. Pass value received from right child to left child.

      3. Compute own value to pass to parent. What is the computation?

   3. Special case for root:
      1. Its value becomes the carry-out (or additional sum bit). Output this value.

      2. Set value to s.

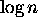   4. descending steps:
      1. Receive value from parent.

      2. Keep first non-p value received (including the value received by a left child from a right child).

7. When finished, all leaves are labeled either s or g. Which is a carry-in of 0 and which is 1?

8. We know no leaf will be ``stuck'' with a p. Why?

9. The carry-in for a leaf is the left-most non-p value to the right of the leaf, as originally computed by the leaves.

   Prove that the algorithm stores this carry in each leaf.