Counterexample, Fixed-Network Connection Model

Tom Kelliher, CS 315

Feb. 8, 1999

Administrivia

Announcements

Assignment

Read Sections 1.2.1, 1.2.2.

Homework due 2/17: Problems 1.2, 1.3, 1.5, 1.7, 1.15.

From Last Time

Lower bound techniques, counterexample.

Outline

1. The counterexample.

2. Properties of the fixed-network connection model.

Coming Up

Carry-lookahead addition, parallel prefix computations.

A Counterexample

Consider sorting within a complete binary tree:

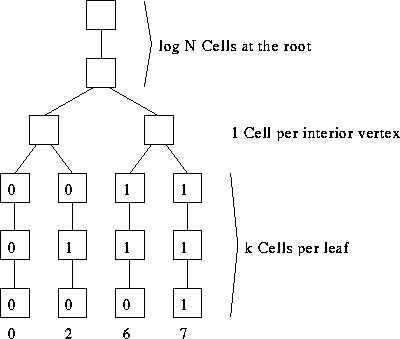
1. Assumption: All bits appear simultaneously.

2. I/O bandwidth? Diameter? Bisection width?

3. Lower bound for sorting on a binary tree?

4. Almost right. Holds for .

5. So, how do we beat the lower bound? By counting.

Example: k=1

1. Problem of unary to binary conversion.

2. ``Easy'' if interior cells are word processors.

3. Each interior processor need only be a serial adder and we do bit-wise serial addition with numbers transmitted lsb-first.

   Example: Bit-wise addition of 0110 and 0011.

4. Example: counting the 1's when N = 8.

5. Setting the leaf bits:
   1. Assume we have m 1's.

   2. Set the rightmost m leaves. Clear the leftmost N - m leaves.

   3. Observation: right 0 leaf is numbered N - 1 - m.

      This is the bit-wise complement of m.

   4. Use N - 1 - m to find a path to that leave, clearing leaves to the left, setting leaves to the right, and clearing that leave.

Generalizing to Larger k

1. Sorting can be done in . What does this tell us?

2. Don't forget: You're counting, not sorting.

Properties of the Fixed-Connection Network Model

1. Processor properties:
   1. Local control.

   2. Computation is a function of local storage and local inputs.

   3. Variations. Processor might know such things as its address, topology/size of the network, time.

      Storage is usually constant, but may vary with size of network.

   4. A bit processor may perform a constant number of bit operations per step. Similarly for a word processor.

   5. Limits on word size usually .

   6. Packets: indivisible communication data stamped with a key.

2. Interconnection properties:
   1. Connections may not vary with time.

   2. A constant amount of communication (bits, words, packets, as appropriate) can occur across a connection per step.

   3. Bounded-degree network. Sometimes degree will be O.

      Size is polynomial in N.

3. I/O protocol properties:
   1. Each input is provided only once.

   2. I/O is when and where oblivious: the time and location, for each piece of data, of I/O must be specified in advance.

      Without this restriction, we could sort in constant time.

4. Comment: This model describes systolic VLSI very well. It doesn't describe general VLSI well since we don't have ``long'' wires. But, how does one model the communication properties of a long wire?