Network properties and a Counterexample
Tom Kelliher, CS 315
Feb. 5, 1999
Will assign homework Monday.
Read 1.2.1, 1.2.2
Linear array sorting example, network properties.
- Network (graph) properties.
- A lower bound counterexample.
- Properties of our fixed-network connection model.
Carry-lookahead addition, parallel prefix computations.
The following are tools we use to establish lower bounds on problems and,
hence, show that a particular parallel algorithm is optimal. As we will
see, they must be applied with care.
Assume the bit model, so we have an 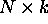 sorting network in the
following.
sorting network in the
following.
- I/O bandwidth.
What is the I/O bandwidth of the sorting network? This makes sorting
 .
.
- Diameter of the network: Defined as the maximum distance between two
vertices in the graph.
What is the diameter of the sorting graph?
Can we construct a sorting problem that will force the two most distant
cells to communicate?
What's the lower bound from this perspective?
- Bisection width of the network: Defined as the number of edges which
must be cut to split the graph in ``half.''
What is the bisection width of the sorting graph?
Can we construct a sorting problem that will force all the data to cross
this boundary?
What's the lower bound from this perspective?
Consider sorting within a complete binary tree:
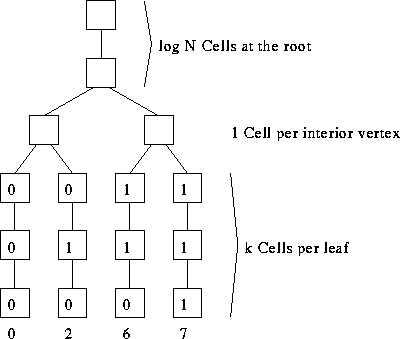
- Assumption: All
 bits appear simultaneously.
bits appear simultaneously.
- I/O bandwidth? Diameter? Bisection width?
- Lower bound for sorting on a binary tree?
- Almost right. Holds for
 .
.
- So, how do we beat the lower bound? By counting.
- Problem of unary to binary conversion.
- ``Easy'' if interior cells are word processors.
- Each interior processor need only be a serial adder and we do
bit-wise serial addition with numbers transmitted lsb-first.
Example: Bit-wise addition of 0110 and 0011.
- Example: counting the 1's when N = 8.
- Setting the leaf bits:
- Assume we have m 1's.
- Set the rightmost m leaves. Clear the leftmost N - m leaves.
- Observation: right 0 leaf is numbered N - 1 - m.
This is the bit-wise complement of m.
- Use N - 1 - m to find a path to that leave, clearing leaves to
the left, setting leaves to the right, and clearing that leave.
- Processor properties:
- Local control.
- Computation is a function of local storage and local inputs.
- Variations. Processor might know such things as its address,
topology/size of the network, time.
Storage is usually constant, but may vary with size of network.
- A bit processor may perform a constant number of bit operations
per step. Similarly for a word processor.
- Limits on word size usually
 .
.
- Packets: indivisible communication data stamped with a key.
- Interconnection properties:
- Connections may not vary with time.
- A constant amount of communication (bits, words, packets, as
appropriate) can occur across a connection per step.
- Bounded-degree network. Sometimes degree will be O
 .
.
Size is polynomial in N.
- I/O protocol properties:
- Each input is provided only once.
- I/O is when and where oblivious: the time and location, for each
piece of data, of I/O must be specified in advance.
Without this restriction, we could sort in constant time.
- Comment: This model describes systolic VLSI very well. It doesn't
describe general VLSI well since we don't have ``long'' wires. But, how
does one model the communication properties of a long wire?
Thomas P. Kelliher
Fri Feb 5 10:06:30 EST 1999
Tom Kelliher
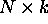 sorting network in the
following.
sorting network in the
following.
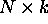 sorting network in the
following.
sorting network in the
following.
 .
.

 bits appear simultaneously.
bits appear simultaneously.
 .
.
 .
.
 .
.