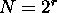 nodes and
nodes and 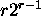 edges.
edges.
Tom Kelliher, CS 315
Apr. 19, 1999
Read openings of 3.1, 3.2, 3.3.
Multiplication, convolution on linear arrays.
Shuffle-Exchanges.
Definition of r-dimensional hypercube:
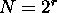 nodes and
nodes and 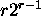 edges.
edges.
Examples: 0- through 4-dimensional hypercubes.
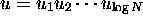 to
node
to
node 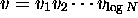 ?
?
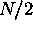 --- remove any
dimension's edges.)
--- remove any
dimension's edges.)
Step: Partition the N-node hypercube into 2 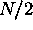 -node hypercubes.
Assume that there is an edge (x010, x110) and, symmetrically, (x011,
x111) in each sub-hypercube, respectively.
-node hypercubes.
Assume that there is an edge (x010, x110) and, symmetrically, (x011,
x111) in each sub-hypercube, respectively.
To construct the linear array for the hypercube, remove those edges and add edges (x010, x011) and (x110, x111).
Definition of r-dimensional butterfly:
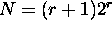 nodes and
nodes and 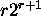 edges.
edges.
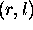 , where r (binary) is the row and l
(decimal) is the level.
, where r (binary) is the row and l
(decimal) is the level.
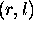 and
and 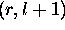 .
.
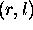 and
and 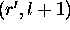 , where r and
, where r and 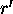 differ only in the lth bit position.
differ only in the lth bit position.
Example: 3-dimensional butterfly.
Observation: Collapsing horizontally, we get the hypercube.
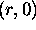 to node (r',l)?
to node (r',l)?
Extend to nodes on arbitrary levels.