Carry-Save Addition
Tom Kelliher, CS 315
Apr. 5, 1999
Read 1.2.4.
Segmented prefix problem.
- Brief review of carry lookahead addition.
- Carry-Save addition.
Multiplication and convolution.
Carrylookahead addition:
- Add two k-bit numbers in
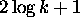 bit steps.
bit steps.
- Suppose we wish to add N k-bit numbers as quickly as possible.
- What is the organization of the adder?
- Do the adders become wider as we progress?
- Running time:
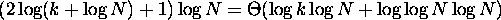
Are these really equivalent?
Can we do better?
- Idea: Add three k-bit numbers in a single bit step, producing two
k+1-bit numbers.
- Implementation: Use a binary full adder for each bit position,
producing a low order bit and a carry bit for each bit position.
- The final sum is the sum of the low order bits and the shifted carry
bits.
- Example:

- Time required to reduce the sum of N k-bit numbers to the sum of
two
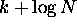 -bit numbers:
-bit numbers: 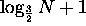 bit steps.
bit steps.
Proof:
- After the first step of CSA, how many numbers are we left with?
(At most
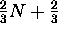 . Why?)
. Why?)
- After the second step?
- After the jth step:

- After
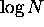 steps, we're left with
steps, we're left with 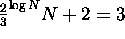 numbers, so we need
numbers, so we need 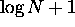 steps to reduce to two
steps to reduce to two 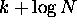 -bit numbers.
-bit numbers.
- Use a carry lookahead adder to reduce the two-number
redundant representation to a single, non-redundant number.
- Example: Draw the Wallace tree for N = 9.
Thomas P. Kelliher
Mon Apr 5 11:02:53 EDT 1999
Tom Kelliher
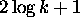 bit steps.
bit steps.
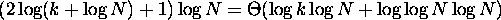
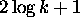 bit steps.
bit steps.
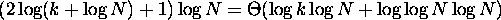

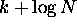 -bit numbers:
-bit numbers: 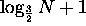 bit steps.
bit steps.
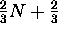 . Why?)
. Why?)

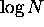 steps, we're left with
steps, we're left with 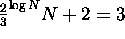 numbers, so we need
numbers, so we need 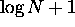 steps to reduce to two
steps to reduce to two 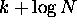 -bit numbers.
-bit numbers.