Performance, Addressing Methods

Tom Kelliher, CS26

Sept. 5, 1996

On-line CPU resources

Performance

For a single program, here's the fundamental equation:

where T is execution time, N is the number of machine instructions to be executed, S is the average number of clock cycles per machine instruction, and R is the clock frequency.

What can we do to improve T?

Memory: Storage and Addressing

1. Bits, bytes, words.
2. k address lines yield addressable locations, numbered .
3. Word addressability, byte addressability.

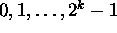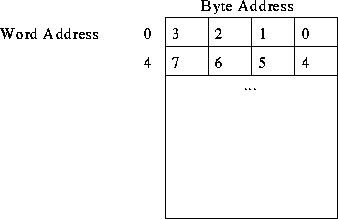
Little-endian byte numbering:

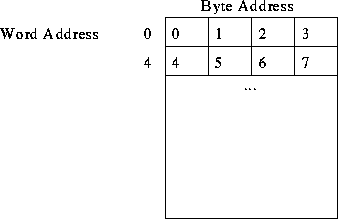
Big-endian byte numbering:

Number Representation

1. Assume 32 bits/word.
2. Bit 0 is lsb; bit 31 is msb.
3. Sign-magnitude representation:

   

4. Two's complement representation:

   

Character Representation

• ASCII, EBCDIC.
• One character per byte.

Instruction Representation

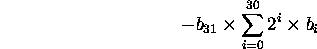
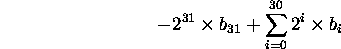
Consider the MIPS instruction

add $16, $17, $18   # R16 = R17 + R18

Instructions and Instruction Sequencing

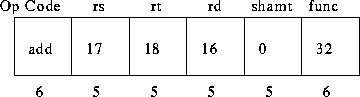
Instruction types:

1. Load/store.
2. Arithmetic and logic.
3. Branch and control.
4. I/O.

Instruction set design choices:

1. Number of addresses: 3, 2, 1, 0.
2. Addressing modes.
3. Fixed vs. variable size instructions, fields
4. Number of general purpose registers

Registers --- the programmer's ``manual cache.''

Number of Address Examples

Consider the C code:

a = b + c;

add a, b, c

load a, r0
load b, r1
add r0, r1, r1
store r1, c

move a, c
add b, c

load a
add b
store c

push a
push b
add
pop c

Straight Line Execution

Simple instruction cycle:

• Instruction fetch: fetch instruction pointed to by PC, update PC (How much?).
• Instruction execute.

Branching

How do you structure a program to add n numbers?

Pseudo C code:

i = n;
sum = 0;
while (i > 0)
   sum += number to be added;

Pseudo assembly:

         move n, r1
         clear r0
loop:    add next number, r0
         decrement r1
         branch >0, loop
         move r0, sum

How does this fit in memory and get executed?

Condition Codes

• N, negative --- set if result is negative.
• Z, zero --- set if result is zero.
• V, overflow --- set if operation overflowed.
• C, carry --- set if carry from msb.

Choices:

1. Condition codes statically set by most/all instructions.
2. No condition codes.
3. Bit in instruction enables setting conditions codes (dynamic).

Effects on performance?

Addressing Modes

Effective address (EA): final location of the operand.

Register Mode

EA is a register, specified in instruction.

add r0, r1

Absolute Mode

EA is a memory location, address specified in instruction.

add data, sum
add 16, 24

Immediate Mode

EA is the instruction --- operand is part of the instruction.

move #0, r0
sub #1, r1

Indirect Mode

EA is memory location pointed to by register or memory word indicated in instruction.

add (r1), r0

Indexed Mode

EA is memory location pointed to by sum of register and a constant (both specified in instruction).

add 12(r0), r1

Not really used for what you think.

Autoincrement, Autodecrement Modes

Stack operations: post-increment, pre-decrement.