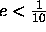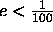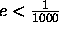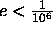Homework 6
CS26
80 pts., due Dec. 5
Show all work.
- (20 pts.)
Represent the decimal values 26, -37, 497, and -123 as signed, 10 bit
numbers in the following binary formats:
- Sign-and-magnitude.
- 1's-complement.
- 2's-complement.
(See Appendix D for decimal-to-binary conversion.)
- (20 pts.)
Binary fractions are discussed briefly in Section 6.10.
- Express the decimal values 0.5, -0.123, -0.75, and -0.1 as signed
6-bit numbers in the binary formats of Problem 1.
- What is the maximum representation error, e, involved in using
only 5 significant bits after the binary point?
- Calculate the number of bits after the binary point so that
-
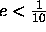
-
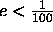
-
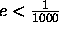
-
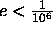
- (20 pts.)
A half-adder is a combinational logic circuit that has two inputs, x and
y, and two outputs, s and c, that are the sum and carry-out,
respectively, resulting from the binary addition of x and y.
- Design a half-adder as a two-level AND-OR circuit.
- Show how to implement a full-adder, as shown in Figure 6.4a, by
using two half-adders and external logic gates.
- Compare the longest path logic delay through the network derived
in part (b) to that of the logic delay of the adder network shown in
Figure 6.4a.
- (20 pts.)
16 of the 4-bit adder circuits shown in Figure 6.7 can be cascaded to form
a 64-bit adder. In this cascade, the output,
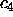 , from the low-order
circuit is connected as the carry-in to the next circuit. Its carry-out,
, from the low-order
circuit is connected as the carry-in to the next circuit. Its carry-out,
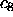 , is connected to the carry-in of the third circuit, and so on. The
circuit has 129 inputs (
, is connected to the carry-in of the third circuit, and so on. The
circuit has 129 inputs (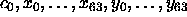 )
and 65 outputs (
)
and 65 outputs (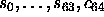 ).
).
- Draw the cascaded circuit. Using the delay model developed in
class, determine the worst-case number of gate delays through the
circuit.
- Using 4-bit adder circuits and 4-bit carry lookahead units,
design a 64-bit full carry lookahead adder. Draw the circuit. Again,
using the delay model developed in class, determine the worst-case
number of gate delays through the circuit.
- Compare the delays. Is the
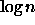 speed-up of the full carry
lookahead adder valid for arbitrarily large values of n? Why or why
not?
speed-up of the full carry
lookahead adder valid for arbitrarily large values of n? Why or why
not?
Thomas P. Kelliher
Mon Nov 25 10:31:19 EST 1996
Tom Kelliher
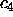 , from the low-order
circuit is connected as the carry-in to the next circuit. Its carry-out,
, from the low-order
circuit is connected as the carry-in to the next circuit. Its carry-out,
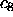 , is connected to the carry-in of the third circuit, and so on. The
circuit has 129 inputs (
, is connected to the carry-in of the third circuit, and so on. The
circuit has 129 inputs (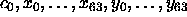 )
and 65 outputs (
)
and 65 outputs (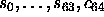 ).
).
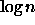 speed-up of the full carry
lookahead adder valid for arbitrarily large values of n? Why or why
not?
speed-up of the full carry
lookahead adder valid for arbitrarily large values of n? Why or why
not?