Homework 5 Solution

CS26

80 pts., due Nov. 21

Show all work.

1. (10 pts.) Consider an ordinary DRAM, a Fast Page Mode DRAM, and an EDO DRAM all rated at the same access speed.
   1. Under what conditions will the Fast Page Mode DRAM be no faster than ordinary DRAM? I.e., characterize the memory access patterns that slow it down.

      When successive memory operations refer to unique rows within the memory cell array.

   2. Are there any memory access patterns that would slow down an EDO DRAM?

      Writes will slow it down. Reads are pipelined.

   3. Characterize the memory access patterns which would cause an interleaved memory to perform no better than a non-interleaved memory.

      When successive memory operations all access the same bank.

2. (10 pts.) In most computers, interrupts are not acknowledged until the current machine instruction completes execution. Consider the possibility of suspending operation of the processor at any point during the execution of an instruction in order to acknowledge an interrupt. Discuss the difficulties that may arise.

   We would have to save numerous pieces of system state to accomplish this:

   1. The value of the instruction step counter.

   2. The values in temporary registers.

   3. The state of memory operations.
   The CPU could probably be designed to save the step counter and temporary registers into a set of ``save'' registers, which the interrupt handler could push onto a stack and later restore to resume the instruction.

   However, how do we deal with pending memory operations? Suppose the CPU is interrupted after issuing a Read, but before issuing the matching WMFC? We would have to be able to re-do some of the previous steps. The control unit would have to be able to deal with these sorts of situations.

   Actually, this is a common situation. Not with interrupts per se, but with page faults in virtual memory systems. Consider the situation where an instruction is fetched just fine, but that instruction references an operand that's not in main memory. A page fault trap is immediately generated to fetch the page into main memory.

3. (10 pts.) Three devices, A, B, and C, are connected to the bus of a computer. I/O transfers for all three devices use interrupt control. Interrupt nesting for devices A and B is not allowed, but interrupt requests from C may be accepted while either A or B is being serviced. Suggest different ways in which this can be accomplished in each of the following cases:
   1. The computer has one interrupt request line.

      When an interrupt from device A or B is being serviced, reset the interrupt enable bits in devices A and B. This prevents nesting of A and B while still allowing C to interrupt. When an interrupt from device C is being serviced, mask out the interrupt line. When the handler has finished servicing A or B, set the enable bits. When C has been serviced, reset the interrupt mask.

   2. Two interrupt request line, INTR1 and INTR2, are available. INTR1 has higher priority.

      Connect the devices so that A and B share INTR2 and C has exclusive use of INTR1. The usual interrupt masking mechanism ensures that interrupt nesting doesn't occur for A and B.

   Specify when and how interrupts are enabled and disabled in each case.

4. (10 pts.) Comment on the following statement: ``Using a faster processor chip results in a corresponding increase in performance of a computer, even if the main memory speed stays the same.''

   If main memory were the performance bottleneck, using a faster CPU wouldn't result in a corresponding performance increase. If the cache system was effective and could keep up with the faster CPU, there would be a corresponding performance increase.

5. (10 pts.) A program consists of two nested loops --- a small inner loop and a much larger outer loop. Here is the general structure of the program:

   

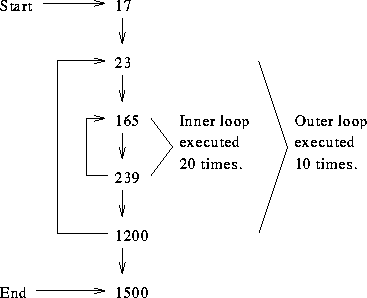
   The memory addresses are in decimal. With the exception of the two branches at addresses 239 and 1200, all instructions utilize straight line sequencing. Each address contains one instruction. The program is to be run on a computer that has an instruction cache organized in the direct-mapped manner and that has the following parameters:

   

   The cycle time of the main memory is 10 s and the cycle time of the cache is 1 s.

   1. Determine the number of bits in the TAG, BLOCK, and WORD fields in main memory addresses.

      Since no mention is made of bytes, assume the memory is word addressable. The main memory is 64K words, so an address is 16 bits. The block size is 128 words, so the WORD field is 7 bits. The cache size is 1K words, so there are 8 cache lines. (size of cache divided by size of block). Therefore, the BLOCK field is 3 bits. The remaining 6 bits is the TAG. Here's how an address is partitioned:

      

   2. Compute the total time needed for instruction fetching during execution of the program.

      On a hit, is spent fetching an instruction. On a miss, 128 words must be fetched from memory, so filling the cache line takes time. I assume that the cache is not a load-through cache, so an additional time is spent transferring a word from the cache to the CPU.

      Here's how the blocks fit into the cache:

      

      Here's how execution proceeds:

         17-22: miss on 17
      
      1st time through outer loop:
         23-164: miss on 128
         165-239: 20 times, no misses
         240-1200: misses on 256, 384, 512, 640, 768, 896, 1024 (replacing
         0-127), 1152 (replacing 128-255)
      
      next 9 times through outer loop:
         23-164: misses on 23 (replacing 1024-1151), 128 (replacing 1152-1279)
         165-239: 20 times, no misses
         240-1200: misses on 1024 (replacing 0-127), 1152 (replacing 128-255)
      
         1201-1500: misses on 1280 (replacement), 1408 (replacement)
      

      Total cache fetches: 26,336 for time. Total misses: 48 for miss penalty of . Total time: .

6. (10 pts.) Consider the effectiveness of interleaving with respect to the size of cache blocks. Using calculations similar to those in Section 5.6.2, estimate the performance improvement for block sizes of 16, 8, and 4 words. Assume that all words loaded into the cache are accessed by the CPU at least once.

   For 16 word blocks, the value of M is . The speed-up is 4.04.

   To properly compare the block sizes, we must bring two 8 word blocks or four 4 word blocks into the cache for each 16 word block. Therefore, for 8 word blocks the value of M is 34 and for 4 word blocks the value of M is . The speed-ups are 3.30 and 2.42, respectively.

   For these three block sizes, a larger block size causes an increase in the hit rate. This hinges upon the assumption that every word brought into the cache is eventually accessed. If this were not the case (and in the real world it's not), we would be wasting effort in transferring large blocks between memory and cache. As one increase block size starting from 1 word, we would expect hit rate to increase with increasing block size until the block size exceeded process locality, at which point the hit rate would begin to decrease as un-accessed words were brought into the cache, replacing words which eventually would be accessed.

7. (20 pts.) A byte-addressable computer has a small data cache capable of holding eight 32-bit words. Each cache block consists of one 32-bit word. When a given program is executed, the processor reads data from the following sequence of hexadecimal addresses: 200, 204, 208, 20C, 2F4, 2F0, 200, 204, 218, 21C, 24C, 2F4

   This pattern is repeated four times.

   1. Show the contents of the cache at the end of each pass through this loop if a direct mapped cache is used. Compute the hit rate for this example. Assume that the cache is initially empty.

      This one is fairly easy. The cache has the same contents after each of the four passes:

      

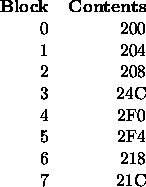
      There are nine misses on the first pass and two misses on each of the subsequent passes. The hit rate is 69%.

   2. Repeat for an associative mapped cache that uses LRU replacement.

      This was more complicated, so I wrote a program. Here's the output:

      Pass 0:
      Misses: 9
      Cache:
      200
      204
      24c
      20c
      2f4
      2f0
      218
      21c
      
      
      Pass 1:
      Misses: 6
      Cache:
      200
      204
      21c
      24c
      2f4
      20c
      2f0
      218
      
      
      Pass 2:
      Misses: 6
      Cache:
      200
      204
      218
      21c
      2f4
      24c
      20c
      2f0
      
      
      Pass 3:
      Misses: 6
      Cache:
      200
      204
      2f0
      218
      2f4
      21c
      24c
      20c
      

      The hit rate was 44%.

   3. Repeat for a four-way set associative cache.

      In the following program output, the first four cache entries are set 0 and the second four entries are set 1.

      Pass 0:
      Misses: 9
      Cache:
      200
      208
      2f0
      218
      204
      24c
      2f4
      21c
      
      
      Pass 1:
      Misses: 3
      Cache:
      200
      208
      2f0
      218
      204
      21c
      2f4
      24c
      
      
      Pass 2:
      Misses: 3
      Cache:
      200
      208
      2f0
      218
      204
      24c
      2f4
      21c
      
      
      Pass 3:
      Misses: 3
      Cache:
      200
      208
      2f0
      218
      204
      21c
      2f4
      24c
      

      The hit rate was 63%.