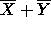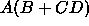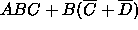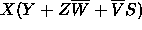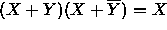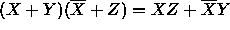Homework 3

CS26

70 pts., due Oct. 17

1. (10 pts.) Design a hall light circuit to the following specification. There is a switch at each end of a hall that controls a single light. If the light is off, changing the position of either switch causes the light to turn on. Similarly, if the light is on, changing the position of either switch causes the light to turn off. Write your assumptions, derive a truth table, and implement the circuit in AND, OR, and NOT gates.

2. (10 pts.) Use DeMorgan's theorem to compute the complement of each of the following Boolean expressions.
   1. 

   2. 

   3. 

   4. 

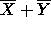
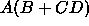
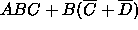
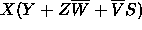
3. (10 pts.) Prove the following simplification theorems.
   1. 

   2. 

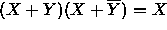
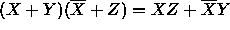
4. (20 pts.) Design a combinational circuit for two-bit binary subtraction. The inputs A, B and C, D form the two two-bit binary numbers N1 and N2. The circuit computes the difference, N1 - N2 on the outputs F (most significant) and G (least significant). Assume that the circuit never sees an input combination in which N1 is less than N2.
   1. Fill in the truth tables for F and G.

   2. Use the K-map method to minimize the realization equations.

   3. Design a circuit implementing the equations using AND, OR, and NOT gates.

5. (20 pts.) Design a combinational circuit with three data inputs D2, D1, D0, two control inputs C1, C0, and two outputs R1, R0. R1 and R0 should be the remainder after dividing the binary number formed from D2, D1, D0 by the binary number formed by C1, C0. For example, if D2, D1, D0 is 111 and C1, C0 is 10, then R1, R0 is 01 (i.e., the remainder of seven divided by two is one). Note that division by zero will never be requested.
   1. Fill in the truth tables for R1, R0.

   2. Use the K-map method to minimize the realization equations. Here's an example of working with a five-variable K-map:

      

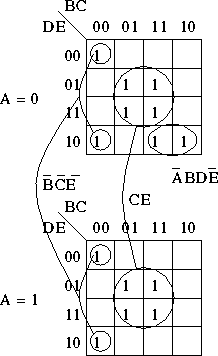
   3. Design a circuit implementing the equations using AND, OR, and NOT gates.