Midterm 2 Solution

CS23

1. Short Answer Problems. Each of the problems is worth 40 points. Please provide a complete, concise answer to each of the following questions.
   1. Write the quicksort algorithm (pseudocode) and show that it is O( n log n) in the average case (i.e., you may assume a ``good'' distribution of the input data).

      1) If the array is smaller than 2 items then return
      
      2) Choose a partition element, p
      
      3) Split array into 2 partitions: p1 and p2
            p1 contains elements < p
            p2 contains elements >= p
            (The array should be placed in the order p1 p p2)
      
      4) Recursively sort p1 and p2
      

      Counting the number of comparisons, Steps 1 and 2 are O(1). Step 3 is O( n). Step 4 is 2O( n/2). Solving the resulting recurrence relation:

      

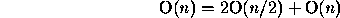
      yields a running time of O( n log n).

   2. With respect to C++ classes, define the following terms: polymorphism, base class, derived class, is-a, and pure virtual function.
      1. Polymorphism: Late binding --- what version of a function to call is not determined until runtime.
      2. Base class: The class from which a derived class inherits properties.
      3. Derived class: The which inherits properties from a base class.
      4. Is-a: Public inheritance --- an operation which is validly applied to an instance of the base class may be applied to an instance of the derived class.
      5. Pure virtual function: A virtual function with no implementation. Its class cannot be instantiated.

   3. You can sort a large array of integers that are in the range 1 to 100 by using an array to count the number of occurrences of each integer in the array.
      1. Implement this sorting algorithm, which is called a bucket sort.

         void bsort(int d[], inst n)
         {
            int counts[100];
            int i;
            int j;
            int cur;
         
            // Empty all the buckets.
            for (i = 0; i < 100; ++i)
               counts[i] = 0;
         
            // "Place" each item from d in its appropriate bucket.
            for (i = 0; i < size; ++i)
               counts[d[i] - 1]++;
         
            // "Take" the items from the buckets, putting them back in d.
            for (cur = 0, i = 0; i < 100; ++i)
               for (j = 0; j < counts[i]; ++j)
                  d[cur++] = i + 1;
         }
         

      2. What is the order of bucket sort?

         O( n).

      3. Why is bucket sort not useful as a general sorting algorithm?

         Generally, you can't bound the range of the inputs. If you have m buckets, then bucket sort is O( m + n). If the range of the inputs is the full range of an int, you have over 4,000,000,000 buckets to examine. Personally, I'd pass on that proposition.

2. Programming Problems. Solve one of the following programming problems. Note that the first problem is not worth as many points as the second problem. You are more likely to receive partial credit if you write your code so that I can understand what you've done.

   Clearly indicate which problem you are solving.

   I suppose I have to solve both of them. Life just isn't fair.

   1. (55 pts.) Write a function, making use of a stack class, which checks to see if a file has all its parenthetical elements ((), {}, []) balanced. Assume that the stack class has been written for you.

      The following are balanced: (), [()]{}.

      The following are unbalanced: ()}, [{}, ([)].

      // Support function.  Match c against top of stack.
      
      int match(Stack &S, int c)
      {
         char d;
      
         if (S.IsEmpty())
            return 0;
      
         S.Top(d);
         S.Pop();
      
         switch (c)
         {
          case ')': return d == '('; break;
          case '}': return d == '{'; break;
          case ']': return d == '['; break;
      
          // This should never happen.
          default: cout << "ARGHHH!\n"; exit(1); break;
         }
      
         // Not reached.
      }
      
      // The function that does the work.  Assumes that f has already been
      // opened.
      
      int checkit(ifstream &f)
      {
         Stack S;
         char c;
      
         while (!f.eof())
         {
            f.get(c);
      
            switch (c)
            {
             case '(':
             case '{':
             case '[': S.Push(c); break;
      
             case ')':
             case '}':
             case ']': if (!match(S, c)) return 0; break;
      
             default: break;
            }
      
         // Stack should be empty at this point.
         return S.IsEmpty();
      }
      

   2. (70 pts.) Using as-a inheritance, implement a stack using a list class. Assume that the list class have been written for you.

      // We have no need for data members in Stack; List provides everyting we
      // need.  However, we don't want a Stack user accessing List methods,
      // so we inherit List privately.
      
      class Stack : private List
      {
       public:
         void Push(int val);
         void Pop(void);
         int Top(void);
         int IsEmpty(void);
      }
      
      void Stack::Push(int val)
      {
         Insert(1, val);
      }
      
      void Stack::Pop(void)
      {
         Delete(1);
      }
      
      int Stack::Top(void)
      {
         return Retrieve(1);
      }
      
      int Stack::IsEmpty(void)
      {
         return List::IsEmpty();   // Scope resolution necessary to prevent
                                   // infinite recursion.
      }