ADT Binary Tree

Tom Kelliher, CS23

May 7, 1997

Nomenclature

A tree:

1. Vertex/node , directed edge.
2. Root, interior vertex, leaf.
3. Parent, child; ancestor, descendant.
4. Siblings.
5. Subtrees.
6. General trees.
7. A Binary tree, T, is a set of nodes such that either:
   • T is empty.
   • T is partitioned into three sets:
     1. A single root.
     2. Two possibly empty sets that are binary trees, the left and right subtrees of the root.
8. Binary search tree:
   • Each vertex has a label. Consider a node labeled r:
     1. If q is in r's left subtree, q is less than r.
     2. If q is in r's right subtree, q is greater than r.
9. Height, level.
10. Full, complete. The book's defn. of complete is wrong. Counterexample?
11. Balanced binary tree, completely balanced binary tree.

Recursive structure.

ADT Tree Operations

• CreateBinaryTree()
• CreateBinaryTree(RootItem)
• CreateBinaryTree(RootItem, LeftTree, RightTree)
• DestroyBinaryTree()
• RootData()
• SetRootData(NewItem)
• AttachLeft(NewItem, Success)
• AttachRight(NewItem, Success)
• AttachLeftSubtree(LeftTree, Success)
• AttachRightSubtree(RightTree, Success)
• DetachLeftSubtree(LeftTree, Success)
• DetachRightSubtree(RightTree, Success)
• LeftSubtree()
• RightSubtree()
• PreorderTraverse(Visit)
• InorderTraverse(Visit)
• PostorderTraverse(Visit)

Traversals

typedef char NodeType;

struct NodeItem
{
   NodeItem* left, right;
   NodeType item;
};

typedef NodeItem* Node;

Preorder

void Preorder(Node T, void (*Visit)(NodeType))
{
   if (T != NULL)
   {
      Visit(T->item);
      Preorder(T->left, Visit);
      Preorder(T->right, Visit);
   }
}

Inorder

void Preorder(Node T, void (*Visit)(NodeType))
{
   if (T != NULL)
   {
      Inorder(T->left, Visit);
      Visit(T->item);
      Inorder(T->right, Visit);
   }
}

Postorder

void Preorder(Node T, void (*Visit)(NodeType))
{
   if (T != NULL)
   {
      Postorder(T->left, Visit);
      Postorder(T->right, Visit);
      Visit(T->item);
   }
}

Examples

void visit(NodeType n)
{
   cout << n << endl;
}

Assume each function is called on the root of:

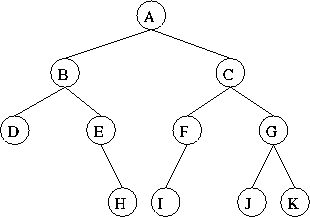
What is printed?

ADT Tree Implementation

Pointer-Based Implementation

Been there, done that.

How do we get to the parent from the child?

Array-Based Implementation

• Tree must be complete.
• Must know number of vertices.

The tree:

char tree[MAXTREE];   // tree[0] is root

children of tree[i]:

• Left child: tree[2 * i + 1]
• Right child: tree[2 * i + 2]

Can get to parent from child.