Tom Kelliher, CS23
Mar. 31, 1997
ADT stack: a fundamental data structure.
Consider evaluating postfix expressions:
23 17 + 18 + 2 5 + 4 2 + * 1 7 4 * + 5 +
An algorithm:
CreateStack()
while not end of line
token = next token from input stream
if token is a number
Push(token, success);
else if token is an operator
GetStackTop(operand1, success)
Pop(operand1, success)
GetStackTop(operand2, success)
Pop(operand2, success)
result = the value of the operator in token applied to
operand1 and operand2
Push(result, success)
else // invalid token
terminate
end_if
end_while
GetStackTop(answer, success)
print answer
DestroyStack()
Where should errors be checked?
stack.h:
#ifndef __STACK_H
#define __STACK_H
#include <stdlib.h>
struct stackItem
{
stackItem* next;
int value;
};
typedef stackItem* stackPtr;
class Stack
{
private:
stackPtr s;
public:
Stack() : s(NULL) {}
~Stack();
Stack(const Stack& oldStack); // copy constructor
int StackIsEmpty(void);
void Push(int newItem, int& success);
void Pop(int& success);
void GetStackTop(int& stackTop, int& success);
};
#endif
stack.cc:
#include "stack.h"
#include <stdlib.h>
#include <assert.h>
Stack::~Stack()
{
stackPtr tmp;
while (s != NULL)
{
tmp = s;
s = s->next;
delete tmp;
tmp = NULL;
}
}
Stack::Stack(const Stack& oldStack)
{
stackPtr oldPtr = oldStack.s;
stackPtr ptr;
if (oldStack.s == NULL)
{
s = NULL;
return;
}
else
{
s = new stackItem;
assert (s != NULL);
ptr = s;
ptr->next = NULL;
ptr->value = oldPtr->value;
oldPtr = oldPtr->next;
}
while (oldPtr != NULL)
{
ptr->next = new stackItem;
assert (ptr->next != NULL);
ptr = ptr->next;
ptr->next = NULL;
ptr->value = oldPtr->value;
oldPtr = oldPtr->next;
}
}
int Stack::StackIsEmpty(void)
{
return s == NULL;
}
void Stack::Push(int newItem, int& success)
{
stackPtr tmp;
tmp = new stackItem;
if (!(success = tmp != NULL))
return;
tmp->value = newItem;
tmp->next = s;
s = tmp;
}
void Stack::Pop(int& success)
{
stackPtr tmp;
if (s == NULL)
success = 0;
else
{
success = 1;
tmp = s;
s = s->next;
delete tmp;
}
}
void Stack::GetStackTop(int& stackTop, int& success)
{
if (s == NULL)
success = 0;
else
{
success = 1;
stackTop = s->value;
}
}
Example usage:
#include "stack.h"
#include <iostream.h>
int main()
{
Stack s;
int tmp, success;
s.Push(2, success); // build s
s.Push(5, success);
Stack t = s; // call copy constructor to make a copy
// different from regular assignment
cout << "s:\n";
s.GetStackTop(tmp, success);
cout << tmp << endl;
s.Pop(success);
s.GetStackTop(tmp, success);
cout << tmp << endl;
s.Pop(success);
cout << s.StackIsEmpty() << endl;
cout << "t:\n";
t.GetStackTop(tmp, success);
cout << tmp << endl;
t.Pop(success);
t.GetStackTop(tmp, success);
cout << tmp << endl;
t.Pop(success);
cout << t.StackIsEmpty() << endl;
return 0;
}
Problem: Finding a set of airline flights to travel from one city to another, if one exists.
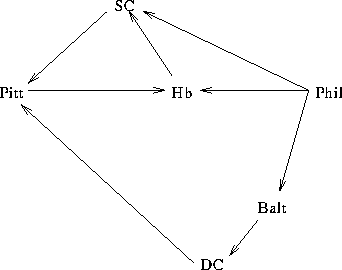
Consider a flight map:

How is it represented?
City file (graph vertices):
Phil Hb SC Pitt Balt DC
Flight file (graph edges):
Phil SC Phil Hb Phil Balt SC Pitt Hb SC Pitt Hb Balt DC DC Pitt
Request file:
Phil DC DC Phil
Implemented as various classes.
read city file, construct names array, visited array,
empty adjacency lists;
read flight file, filling adjacency lists to construct flight map;
open request file;
while there is a request
{
check its validity;
mark departure point visited and push onto stack;
while the stack is not empty and the destination
is not on top of stack
{
if there are no unvisited cities on the adjacency list for
the top of stack city
pop it from the stack;
else
mark that city as visited and push onto stack;
}
if the stack is empty
no flight path exists
else
print the flight path
What does recursion use?
What data structure is used for activation records?