Loop Invariants

Tom Kelliher, CS23

Feb. 12, 1997

Loop Invariants

Four characteristics:

Must be true upon entry into the loop
Execution of the loop body must preserve the invariant
Invariant must capture the correctness and the meaning of the loop
Loop must terminate

Consider the code:

const int SIZE = 100;
int data[SIZE];
int i;
int sum;

// stuff to initialize data

sum = 0;
for (i = 0; i < SIZE; i++)
   sum += data[i];

cout << "Sum: " << sum << endl;

Here's the invariant:

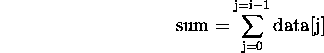
Note that this and the loop condition imply that when the loop terminates, the first SIZE elements of data have been summed.

Three more examples:

prod = 1;
for (i = 0; i < n; i++)
   prod *= n;

Here's the invariant:

This and the loop condition imply that prod has a final value of .

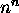void SelectionSort(dataType A[], int N)
{
   for (int Last = N-1; Last >= 1; --Last)
   {
      // select largest item in A[0..Last]
      int L = IndexOfLargest(A, Last+1);

      // swap largest item A[L] with A[Last]
      Swap(A[L], A[Last]);
   }  // end for
}  // end SelectionSort

Here's the invariant (I'm assuming that the elements of A are unique):

Elements A[Last + 1] through A[N - 1] are in ascending order and each of those elements is larger than any of the elements A[0] through A[Last].

This and the loop condition imply that the N elements of A are sorted into ascending order when the loop finishes.

int IndexOfLargest(const dataType A[], int Size)
{
   int IndexSoFar = 0;  // index of largest item found so far

   for (int CurrentIndex = 1; CurrentIndex < Size;
                              ++CurrentIndex)
   {
      if (A[CurrentIndex] > A[IndexSoFar])
         IndexSoFar = CurrentIndex;
   }  // end for

   return IndexSoFar;  // index of largest item
}  // end IndexOfLargest

Here's the invariant:

IndexSoFar is the index of the largest element in A[0] through A[CurrentIndex - 1].

Note that this implies that IndexSoFar is the index of the largest element among the first Size elements of A when the loop terminates.

Student Exercises

See also the loop invariant solution to the student exercises. This will be posted to the class home page.

Thomas P. Kelliher
Mon Feb 10 15:46:08 EST 1997

Tom Kelliher