Sorting Algorithms

Tom Kelliher, CS23

Apr. 23, 1997

Solve the recurrences:

The Three ``Slow'' Sorts

• Bubble sort.
• Selection sort.
• Insertion sort.

How slow are they?

What distinguishes them?

Lower Bound for Comparison-Based Sorting

Stirling's approximation:

Permutations and decision trees:

Mergesort

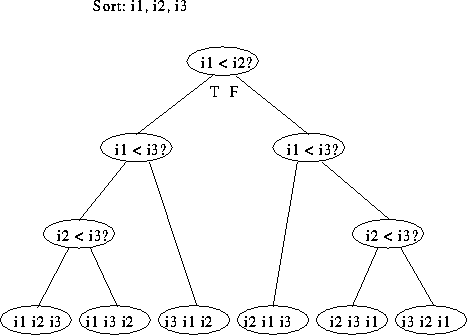
Algorithm:

Split the array, A, into two pieces, A1 and A2
Recursively sort each piece

Empty A

while neither A1 nor A2 is empty
   if the first item in A1 is smaller than the first item in A2
      add A1's item to the end of A, removing it from A1
   else
      Add A2's item to the end of A, removing it from A2
   end_if
end_while

one of A1, A2 is not empty -- move its elements to the end of A

See the home page for an implementation.

Efficiency:

• Number of comparisons.
• Memory used.

Internal/External sorting method.

Quicksort

• Worst-case, average-case.
• Pivot Selection.
• Key: efficiency of partitioning.

Algorithm:

QuickSort(A[], f, l)
{
   if (f < l)
   {
      choose a pivot, p, from A[f...l]
      partition A about p

      // index of p is pIndex

      QuickSort(A, f, pIndex - 1)
      QuickSort(A, pIndex, l)
   }
}

Satisfaction of recursive requirements?

Selection of the Pivot Value

What happens if one of the partitions is always empty?

How can we guarantee a ``good'' pivot value?

Partitioning the Array

/**********************************************************************
 * Precondition: A has len elements and A[0] is the desired pivot
 * element.
 *
 * Postcondition: Returns the index, s, of the pivot element.
 * A[i] < A[s] for 0 <= i < s and A[s] <= A[j] for s < j < len.
 **********************************************************************/

int partition(int A[], int len)
{
   int s = 1;
   int l = len - 1;

   // invariant: A[i] < A[0] for 1 <= i < s and
   //            A[0] <= A[j] for l < j < len.
   while (s < l)
   {
      if (A[s] < A[0])   // A[s] belongs in first partition.
         ++s;
      else   // A[s] belongs in second partition: make room.
      {
         swap(A[s], A[l]);
         --l;
      }
   }
   
   // A[s] could either be in first or second partition.
   if (A[s] >= A[0])   // A[s] is in second partition --- don't move it.
      --s;

   swap(A[0], A[s]);   // Swap partition element with last element in
                       // first partition.
   return s;
}

Number of comparisons?

Radix (Bucket) Sorting

Consider sorting ``constant width'' numbers.

Constant time sort.

Bucket implementation.