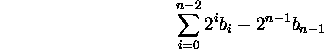Number Representation
Tom Kelliher, CS 220
Sept. 29, 1997
Review on Wednesday.
Read Chapter 4.
Numerous ways of representing a value. Selection criteria:
- Ease of implementing: addition, negation (subtraction), comparison.
- Symmetry.
- Speed.
- Hardware requirements.
One of the ``holy wars'' in architecture:
- Memory is byte addressable.
- A word is multiple bytes/bits.
- How are the bytes/bits numbered?
- Little endian.
- Big endian.
Bit numbering: 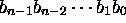
For examples, assume b = 8.
Unsigned value of an binary integer:

Maximum, minimum values and representations?
Msb is the sign bit:
- Has no weight.
- If 0, the number is ``positive.''
- If 1, the number is ``negative.''
- Value:

- Problems:
- Multiple representations of 0.
- Hard to build good adders.
- Minimum, maximum values and representations?
- Symmetric range.
- Sign extension. Why is this important?
Msb is the sign bit:
- Has negative weight:
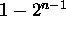 .
.
- If 0, the number is ``positive.''
- If 1, the number is ``negative.''
- One's complement:
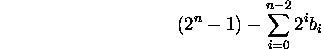
- Value:
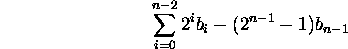
How did we get the weight for 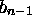 ?
?
- Problems:
- Multiple representations of 0.
- Wrap-around carrys.
- Minimum, maximum values and representations?
- Symmetric range.
- Sign extension.
Msb is the sign bit:
- Has negative weight:
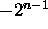 .
.
- If 0, the number is ``positive.''
- If 1, the number is ``negative.''
- Two's complement:

One's complement plus one.
- Value:
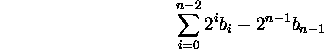
- Problems:
- Asymmetric range.
- Minimum, maximum values and representations?
- Sign extension. Why does this work?
- Add a bias to a value to get the representation.
- Bias 127: add 127 to value.
- value:

where B is the bias.
- Minimum, maximum values and representations?
- Used for exponent representation in floating point.
Represent each of the following in sign-magnitude, one's complement,
two's complement, and bias 127 form: 1, -1, 127, -127, 128, -128, 45, -45.
- ASCII.
- One character per byte.
- Packed formats --- importance of shifts.
Thomas P. Kelliher
Mon Sep 29 08:09:06 EDT 1997
Tom Kelliher
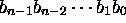
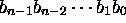


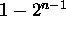 .
.
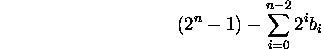
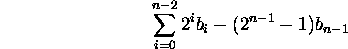
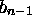 ?
?
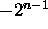 .
.