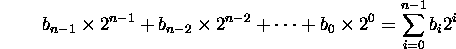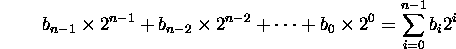Number Representation
Tom Kelliher, CS 220
Sept. 26, 1997
Midterm in one week.
Problems 3.8, 3.10, and 3.13. For problem 3.13, replace fraction
with non-integer.
Properties of conventional number systems:
- Positional.
- Weighted.
- Radix/Base.
- Most significant, least significant.
Unsigned value of a binary integer:
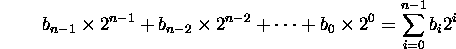
- n bit number.
- Bit numbering.
Common bases: decimal, binary, octal, hexadecimal.
Use the previous summation and do all math in decimal.
Example: convert binary 110101 to decimal.
(How well do you know your powers of 2?)
Algorithm:
let dnum be the decimal number to convert;
index = 0;
bnum = 0;
while (dnum != 0)
{
bnum[index] = dnum % 2;
dnum = dnum / 2;
index = index + 1;
}
Example: convert decimal 133 to binary.


Form for octal & hexadecimal constants in C?
Conversion examples?
- Fractional powers of 2.
- Converting a fractional binary number to decimal.
- Using the algorithm to convert a decimal integer to a binary integer
as a starting point, develop an algorithm to convert a decimal fraction to a
binary fraction.
- Examples.
- Scientific notation: mantissa and exponent.
- Normalization:
- Floating point mantissas are fractions.
- Normalized range:

- Why bother with normalizing?
- Gradual underflow and de-normalized numbers.
- The IEEE standard.
- Density of representable values on the number line.
- Quantization error.
- Precision and Accuracy.
Thomas P. Kelliher
Thu Sep 25 17:39:32 EDT 1997
Tom Kelliher