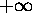Additional Arithmetic

Tom Kelliher, CS 220

Oct. 17, 1997

Announcements

Final: 12:00--2:00pm on 12/18/97 in HS 149.

Collect homework.

Assignment

Read Pentium Pro: A Tour of the Microarchitecture
(http://www.intel.com/procs/ppro/info/p6white/index.htm).

Notes on the New Homework

Consider a block diagram picture of unsigned integer multiplication via multiplicand shift:

1. Two memory words to store multiplicand and product.

2. How do you shift the multiplicand?

3. How do you detect and handle carry from lsw to msw of product?

4. How do you examine successive multiplier bits?

Division

Similar to multiplication: shift and subtract --- paper and pencil division.

Hard to speed up.

Algorithm:

quotientMask = 0x1;
count = 0;
quotient = 0;

while (dividend >= divisor)
{
   ++count;
   quotientMask <<= 1;   // << is the shift operator in C
   divisor <<= 1;
}

--count;
quotientMask >>= 1;
divisor >>= 1;

for ( ; count >= 0; --count)
{
   if (dividend >= divisor)
   {
      quotient |= quotientMask;
      dividend -= divisor;
   }

   quotientMask >>= 1;
   divisor >>= 1;
}

remainder = dividend;

Floating Point Arithmetic

Addition/Subtraction

Algorithm:

1. If applicable, convert subtraction to addition.

2. Align significands.

3. Add significands (mantissas). Sign goo.

4. Normalize.

Issues:

1. How many shifts required to normalize? What direction?

2. Can we over/underflow?

Multiplication

Algorithm:

1. Multiply significands.

2. Add exponents. (whoops).

3. Normalize.

4. Set sign.

Issues:

1. How many shifts required to normalize? What direction?

2. Can we over/underflow?

Division

Issues:

1. How many shifts required to normalize? What direction?

2. Can we over/underflow?

Maintaining Precision

Rounding methods:

1. Truncate.

2. Round to .

3. Round to .

4. Round to nearest even.

Hardware assists:

1. Use of intermediate forms with additional precision.

2. Round, guard bits.

3. Sticky bit.

Comment: Floating point arithmetic is not associative. Consider:

double result1, result2;

result1 = (MAXDOUBLE + -MAXDOUBLE) + 1.0;   // = 1.0
result2 = MAXDOUBLE + (-MAXDOUBLE + 1.0);   // = 0.0