Addition, Subtraction, and Multiplication
Tom Kelliher, CS 220
Oct. 15, 1997
Start reading Chapter 6.
Addition algorithm for a plus b:
if a and b are of the same sign
{
sign of sum = sign of a;
magnitude of sum = magnitude of a + magnitude of b;
}
else if magnitude of a > magnitude of b
{
sign of sum = sign of a;
magnitude of sum = magnitude of a - magnitude of b;
}
else
{
sign of sum = sign of b;
magnitude of sum = magnitude of b - magnitude of a;
}
How do we handle subtraction?
Comparison slows this. Can we speed it up?
When can overflow occur? How do we detect it?
- Two's complement representation for n-bit numbers and the face of a
clock with
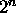 positions.
positions.
- An n-bit adder adds modulo
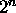 .
.
- Addition examples for n=4:
- -4, 2.
- -2, 4.
- 3, 4.
- -3, -4.
- 4, 4.
- So, what's the addition algorithm?
- How do we subtract? Given a four-bit adder circuit, design an
adder/subtractor.
- How do we detect overflow?
- The addition wheel.
- Adding one to skip the second zero.
- The wraparound carry in adder circuits.
- Paper and pencil multiplication: shift the multiplicand and scale by
the appropriate multiplier bit.
- Unsigned binary example:
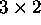 in 3 bits.
in 3 bits.
- n-bit multiplicand, multiplier: 2n-bit result.
- Signed binary multiplication: sign-extend multiplicand multiplier to
2n bits.
- Examples in 3 bits:
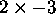 ,
, 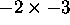 .
.
Consequences:
- 2n-bit adder required.
- 2n bits of storage each required for multiplicand and partial
product.
- n-bits of storage required for multiplier. (Why only n bits?)
- Next homework problem: Pseudo-code and SAL to multiply two 32-bit
signed integers, producing a 64-bit result, by shifting the multiplicand.
Observation: shifting multiplicand left is equivalent to shifting partial
product right.
Consequences:
- Only an n-bit adder required.
- 2n bits of storage required for partial product.
- n bits of storage each required for multiplicand and multiplier.
Algorithm:
ms_sum = ls_sum = 0;
for (i = 0; i < 32; ++i)
{
if (lsb of multiplier == 1)
ms_sum += multiplicand;
shift multiplier right one bit;
shift ls_sum right one bit;
if (lsb of ms_sum == 1)
set msb of ls_sum;
shift ms_sum right one bit;
}
Thomas P. Kelliher
Wed Oct 15 07:53:40 EDT 1997
Tom Kelliher
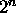 positions.
positions.
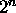 .
.
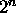 positions.
positions.
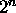 .
.
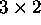 in 3 bits.
in 3 bits.
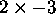 ,
, 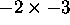 .
.