Shifting Operations; Arithmetic

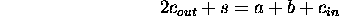
Tom Kelliher, CS 220

Oct. 13, 1997

Announcements

Assignment

Finish reading Chapter 5. Homework handout.

Shifting Operations

1. Logical shifts: sll and srl.

2. Arithmetic shifts: sra.
   1. Where's sla?

   2. Can I really use these to divide/multiply?

3. Rotates: ror and rol. Redundant.

Addition and Subtraction

Examples. Add the unsigned binary numbers 10111110 and 00010011. Add 01111111 and 00000001.

Idea: a modular one-bit adder.

What are the inputs? The outputs?

The rule to be satisfied:

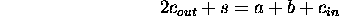
Truth table for binary addition:

Alternate ways of viewing the outputs?

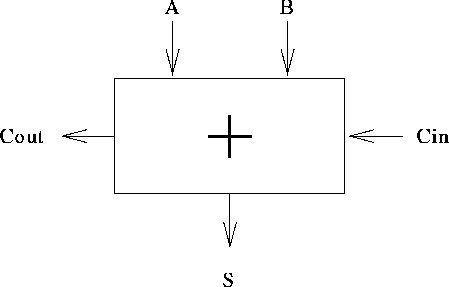
A one-bit adder:

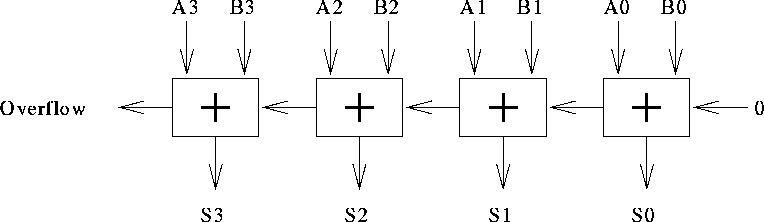
A four-bit adder from four one-bit adders:

Addition can be pretty slow. Some useful definitions:

1. Carry generate:

   

2. Carry propagate:

   

Carry-Lookahead Equations:

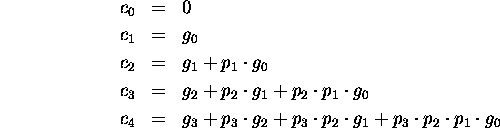
Compare to the text.

Sign-Magnitude

Addition algorithm for a plus b:

if a and b are of the same sign
{
   sign of sum = sign of a;
   magnitude of sum = magnitude of a + magnitude of b;
}
else if magnitude of a > magnitude of b
{
   sign of sum = sign of a;
   magnitude of sum = magnitude of a - magnitude of b;
}
else
{
   sign of sum = sign of b;
   magnitude of sum = magnitude of b - magnitude of a;
}

Comparison slows this. Can we speed it up?

When can overflow occur? How do we detect it?

Two's-Complement

1. Two's complement representation for n-bit numbers and the face of a clock with positions.

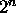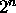2. An n-bit adder adds modulo .

3. Addition examples for n=4:
   1. -4, 2.

   2. -2, 4.

   3. 3, 4.

   4. -3, -4.

   5. 4, 4.

4. So, what's the addition algorithm?

5. How do we subtract? Given a four-bit adder circuit, design an adder/subtractor.

6. How do we detect overflow?

One's Complement

1. The addition wheel.

2. Adding one to skip the second zero.

3. The wraparound carry in adder circuits.