Fundamental Data Types and Conversions

Tom Kelliher, CS18

Mar. 1, 1996

Fundamental Data Types

Integer Types

char, int

Attributes:

• signed/ unsigned (does not affect memory allocated)
• int is signed by default
• Default for char is implementation dependent
• short/ long (applicable to int only)

Note:

• char can store an integer
• int can store an ASCII value
• Strings must be stored in char[]

Memory allocation:

Representation Ranges (Repeat)

Signed, unsigned two's complement representation

Consider the eight bit number: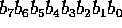

Signed value: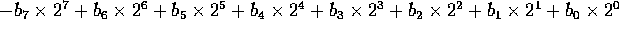

Unsigned value: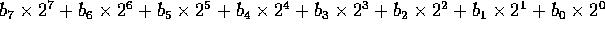

Examples:

• 01010101
• 11111001
• 01101001
• 10000101

Smallest, largest values for each representation?

How many unique values can be represented by n bits?

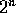, proven by induction on n

Basis: n = 1

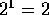and a one bit number has two unique values: 0 and 1.

Inductive Step: Assume that 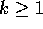bits can represent 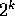values, show that k+1 bits can represent 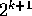values.

k+1 bit numbers can be broken into 2 groups:

• 0<k bits>
• 1<k bits>

Counting and using the inductive hypothesis, there are 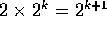k+1 bit numbers. QED.

Formulas for ranges of n-bit numbers?

Floating Point Types

Memory allocation:

float, double, long double

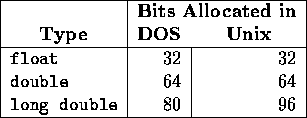
Precision:

• float: 6 decimal digits
• double, long double: 15 digits

Range:

• float: 1.17E-38--3.4E+38
• double, long double: 2.22E-308--1.79E+308

Common Runtime and Design Errors

• Division by 0
• Integer division
• Arithmetic overflow
  • Integer: ``Wraparound''

    Consider 4 bit signed/unsigned numbers

  • Floating point: NaN
• Arithmetic underflow
• Representational errors
• Cancellation errors:

  #include <iostream.h>
  
  int main()
  {
     double little = 1.0E-10;
     double middle = 1.0E4;
     double big = 1.0E6;
     double bigger = 1.0E7;
  
     cout << (middle + little) - middle << endl;
     cout << (big + little) - big << endl;
     cout << (bigger + little) - bigger << endl;
  
     return 0;
  }
  

  Output:

  1.00044e-10
  1.16415e-10
  0
  

Type Conversions

Expression types:

• Assignment expression --- type of the left operand; right hand value implicitly cast if need be
• All other expressions --- largest of int and the types of the two operands. Operator is resolved to this type

Relative ``sizes'' of types:

1. signed int
2. unsigned int
3. signed long int
4. unsigned long int
5. float
6. double
7. long double

Note: range increasing

Assignment conversion to ``smaller'' type unsafe (?)

Given the declarations, determines the expression types and the ``safeness:''

int a;
unsigned int b;
char c;
float x;
double y;
long double z;

c = a % b - 5;
x = c - b * a;
b = c * c + b * a / 3;
a = y - c * a % b;
x = y * z;
c = +x * -y + 7 / z;
x = ((x - 6) * (x - 6) + y * y) / (z * z);
x += c + z;