Tom Kelliher, CS18
Feb. 28, 1996
Things to notice:
Similarities to homework program?
int BinSearch(const int A[], int First, int Last,
int Value)
{
if (First > Last)
return -1; // Value not in original array
else
{ // Invariant: If Value is in A,
// A[First] <= Value <= A[Last]
int Mid = (First + Last)/2;
if (Value == A[Mid])
return Mid; // Value found at A[Mid]
else if (Value < A[Mid])
return BinSearch(A, First, Mid-1, Value); // X
else
return BinSearch(A, Mid+1, Last, Value); // Y
} // end else
} // end BinSearch
Costs:
Consider:
int fib(int val)
{
if (val <= 2)
return 1;
else
return fib(val - 1) + fib(val - 2);
}
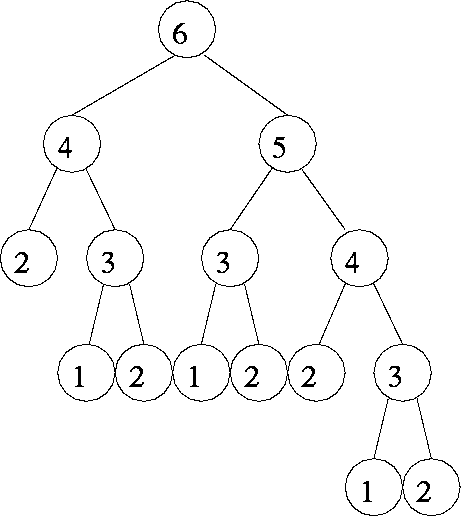
Call graph for fib(6):

A function is tail recursive if the very last thing it does is make its recursive call.
Example:
void printLinkedList(list* l)
{
if (l != NULL)
{
cout << l->fname << " " << l->lname << endl;
printLinkedList(l->next);
}
}
Recall:
int fact(int n)
{
if (n <= 1)
return 1;
else
return n * fact(n - 1);
}
Are fact(), fib() tail recursive?
What is it?
Write a recursive function which prints a reversed string
void reverse(char* s)
{
if (*s != '\0')
{
reverse(s + 1);
cout << *s;
}
}
Is it head recursive?
Utility of head recursion
Write a recursive function which computes pow(n, i).
int pow(int n, int i)
{
if (i == 0)
return 1;
else if (i == 1)
return n;
else
{
int partial = pow(n, i / 2);
if (i % 2 == 0)
return partial * partial;
else
return partial * partial * n;
}
}
More efficient than iterative solution?
To work on the homework program