Introduction to Recursion

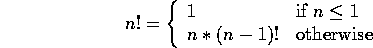
Tom Kelliher, CS18

Feb. 23, 1996

Recursion

What is it?

A function that calls itself directly or indirectly to solve a smaller version of its task until a final call which does not require a self-call is a recursive function.

Divide and conquer approach

What do I need?

1. Decomposition into smaller problems of same type
2. Recursive calls must diminish problem size
3. Necessity of base case
4. Base case must be reached

Binary Search Algorithm

Looking up a word in the dictionary?

• Sequential search
• Binary search

Algorithm:

Search(dictionary)
{
   if (Dictionary has only 1 page)
      Sequentially search page for word
   else
   {
      Open the dictionary to the middle page
      Determine which half of the dictionary the word is in

      if (The word is in the first half)
         Search(first half of dictionary)   // ignore second half
      else
         Search(second half of dictionary   // ignore first half
   }
}

Dictionary structure?

Compare to sequential search

Factorial

Meet requirements?

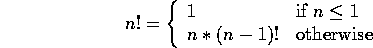
Consider the code fragment:

main()
{
   int i = 3;                 // 1
   cout << f(i) << endl;      // 2
}

int f(int a1)
{
   if (a1 <= 1)               // 3
      return 1;               // 4
   else                       // 5
      return a1 * f(a1 - 1);  // 6
}

Non-recursive version:

int fact(int n)
{
   int i;
   int prod = 1;

   for (i = 1; i <= n; i++)
      prod *= i;

   return prod;
}

The Fibonacci Sequence

Definition:

Consider:

int fib(int val)
{
   if (val <= 2)
      return 1;
   else
      return fib(val - 1) + fib(val - 2);
}

Call graph for fib(6):

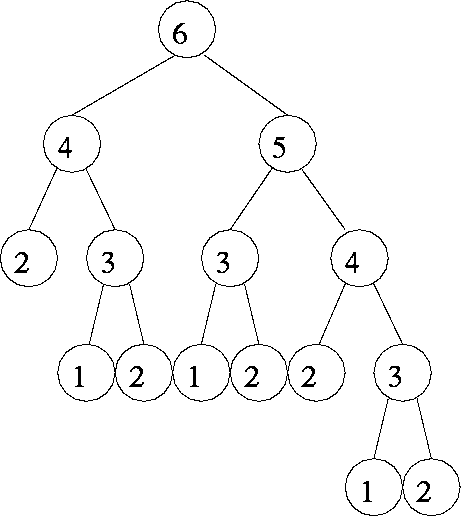
Non-recursive version:

int fib(int val)
{
   int current = 1;
   int old = 1;
   int older = 1;

   val -=2;

   while (val > 0)
   {
      current = old + older;
      older = old;
      old = current;
      --val;
   }

   return current;
}

Greatest Common Divisor

Definition:

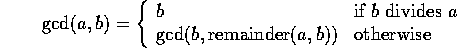
int gcd(int a, int b)
{
   int remainder = a % b;

   if (remaider == 0)
      return b;
   else
      return gcd(b, remainder);
}

Fun with an Array

What does this do?

int main()
{
   int array[4] = { 1, 2, 3, 4 };

   mystery(array, 4);
}

void mystery(int array[], int size)
{
   if (size > 0)
   {
      --size;
      cout << array[size] << endl;
      mystery(array, size);
   }
}

How about this?

int mystery(int array[], int size)
{
   --size;

   if (size > 0)
      return a[size] + mystery(array, size);
   else
      return a[size];
}

Exercise

Write a recursive function which finds the maximum value stored in an int array.