Foundations, Sorting on a Linear Array, Algorithm Assessment

Tom Kelliher, CS 315

Jan. 25, 1999

Administrivia

Announcements

Assignment

Read Section 1.1.1--1.1.3.

From Last Time

Foundations: asymptotic analysis, mathematical induction.

Outline

1. Foundations: loop invariants.

2. Sorting on a linear array: linear arrays, sorting, time analysis.

3. Algorithm assessment.

Coming Up

Using fewer processors, the bit model, lower bounds.

Foundations

Loop Invariants

Four characteristics:

1. Must be true upon entry into the loop
2. Execution of the loop body must preserve the invariant
3. Invariant must capture the correctness and the meaning of the loop
4. Loop must terminate

Consider the following sorting algorithm which sorts the n elements of data (the elements are indexed ):

      for i := n downto 2 do
         largest := i;
      
         for j := i-1 downto 1 do
            if data[j] > data[largest]
               largest := j;
      
         swap(data[largest], data[i]);

Prove that the algorithm sorts the elements of the array data into ascending order.

First, demonstrate the algorithm on the array

int data[] = { 12, 19, 6, 15 };

Sorting on a Linear Array

Linear Arrays

A linear array:

Cell properties:

1. Local program: a ``few'' operations.

2. Local storage: a ``few'' words of data.

3. Operation sequence:
   1. Receive inputs from neighbors.

   2. Read local storage.

   3. Perform computation indicated by local program.

   4. Generate output for neighbors.

   5. Update local storage.

4. Synchronized to a global clock.

5. Must all the programs be identical? Elegance?

Communication properties:

1. Bidirectional links between cells.

2. Left, right neighbors.

3. Fixed connection network.

4. Data pulsing through network: systolic computation.

Sorting

1. Phase 1: sorting program.
   1. Accept input from left neighbor.

   2. Compare to stored value.

   3. Output larger value to right neighbor.

   4. Store smaller value.

2. Phase 2: output. Begin passing left when no more input is received from the left neighbor.

Example: sort 12, 19, 6, 15.

How many steps to sort? How many steps to output?

Algorithm Assessment

How can we measure a parallel algorithm? Apply following to sorting on the linear array.

1. Run time: T.

2. Number of processors: N.

3. Speedup: Let be the running time of the fastest sequential algorithm. Then:

   

   What is linear speedup?

   Say you have P processors. Speedup is at most P. Why? (Hint: a parallel algorithm that runs in T steps on P processors can be simulated on a sequential machine in how many steps?)

4. Work: W = TP.

   Measures algorithm inefficiencies due to idle processors.

5. Efficiency of processor utilization:

   

6. Is it always possible to minimize T and E?

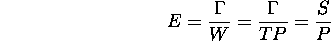
   Example: consider two algorithms for solving a problem of size M:

   1. M steps on an M processor machine.

   2. steps on an processor machine.

   If we have an processor machine and need to run the algorithm X times, which algorithm should we use? Assume the processor machine may be split in M M processor machines.

   (Recall: .)