Combinational Logic Circuits
Tom Kelliher, CS26
Sept. 26, 1996












Applying logical operations to bytes, words, etc., on a bit-by-bit
basis.
Example:
- Register $8 contains 0x123.
- Register $9 contains 0xABC.
- Result of
and $10, $8, $9
- Result of
or $10, $8, $9
- How would you clear a bit or set of bits in a word?
- How would you set a bit or set of bits in a word?
- Given a logic expression, how do we implement it?
- Every Boolean expression can be represented in sum of
products form.
- Implementing SOP expressions.
- Limitations.
Convert each of the following to SOP notation and draw a logic circuit,
using AND, OR, and inverter gates, implementing it:
-
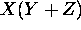 .
.
- XY + YZ.
-
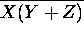 .
.
-
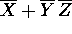 .
.
- Implement a binary full adder. Here is the truth table:

Start by writing the SOP equation.
BTW, is this a useful function?
- Consider a five-input Boolean function that is asserted whenever
exactly two of its inputs are asserted. Construct its truth table, its
SOP equation, and an implementation.
Why bother? Speed, power, real estate.
Minimization Techniques:
- Quine-McCluskey.
- Karnaugh Maps.
- Espresso.
Two-variable example:

- Minimal cover.
- The map is a torus.
- Don't cares in real circuits.
- Gray code numbering.
- Converting the covers to equations.
Try the following:
- The sum output of a full binary adder.
- The carry out output of a full binary adder.
- A circuit which compares two-bit unsigned numbers. There are three
outputs: inputs equal, first greater, second greater.
Why do TTL and CMOS designers use these gates?
Why are ECL designers so lucky?
Thomas P. Kelliher
Wed Sep 25 16:03:38 EDT 1996
Tom Kelliher













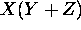 .
.
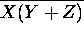 .
.
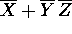 .
.

